La musique vue par une mathématicienne

À la base de toute musique est le son. Qu'est-ce qu'un son? Si on entend un son, c'est que la membrane de notre oreille a détecté une onde dans l'air. Une telle onde est créée par un changement de pression dans l'air, ce qui peut être produit par exemple par une corde en vibration. Une corde qui vibre pousse les molécules d'air en les déplaçant, ce qui crée des endroits de haute pression et, par conséquent, des endroits de basse pression aussi. Les molécules déplacées avant de revenir à leurs positions bousculent les autres molécules en faisant  propager l'onde dans l'espace vers nos oreilles. 

Une onde sonore est caractérisée mathématiquement par son amplitude et sa fréquence. L'amplitude est reliée au volume du son tandis que la fréquence caractérise le ton du son que l'on entend.

C'est la fréquence qui a été le point focal des réflexions mathématiques sur la musique depuis le temps de Pythagore (6ième siècle avant J.-C.). Prenons un point sur la corde. Pendant que la corde vibre, ce point atteint de temps en temps sa hauteur maximale. La fréquence, mesurée en Hertz, nous dit combien de fois par seconde la hauteur maximale est atteinte par ce point (évidemment, ce nombre ne dépend pas du point choisi sur la corde). Par exemple, la corde produit le son associé à la note «la» si elle vibre à la fréquence de 440 Hertz, c'est-à-dire que la crête sur la corde apparaît  440 fois par seconde.

En réalité, le son produit par une corde en vibration est composé de plusieurs fréquences, mais parmi elles il y en a une fondamentale (ou premier harmonique). Les autres s'appellent harmoniques de rang supérieur. La fréquence fondamentale a la contribution la plus importante au son qu'on entend et c'est elle qui est associée à la note musicale correspondante. Une corde dont la fréquence fondamentale est égale à X Hertz, vibre aussi avec les fréquences harmoniques 2X Hertz, 3X Hertz, 4X Hertz et ainsi de suite.

Comme on le sait bien, la musique occidentale (la seule dont on parle dans ce texte) est basée sur une gamme comportant douze notes, douze demi-tons, ce qui est illustré par l'image d'un clavier de piano.

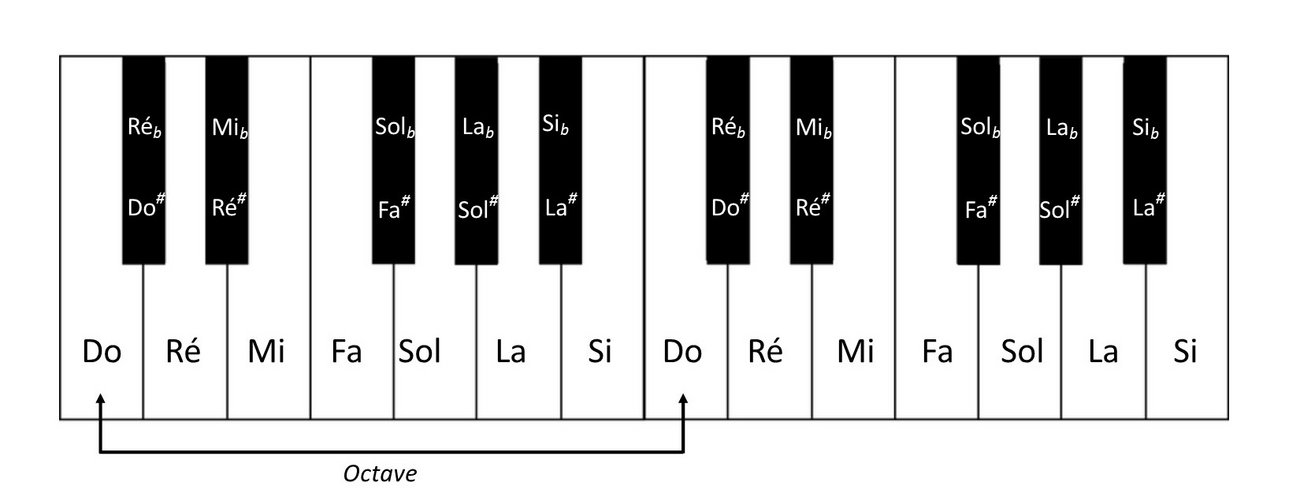
Toute la musique que nous connaissons est faite de sept notes do, ré, mi, fa, sol, la si (clés blanches) et cinq notes altérées (clés noires). La partie entre deux notes de même nom les plus proches l'une à l'autre est une octave. De nos jours, chaque note est associée à une fréquence bien définie, mais ce n'était pas toujours ainsi. En variant la longueur d'une corde on peut varier sa fréquence fondamentale. La note « do » a toujours servi de référence. Elle n'a pas toujours été associée à une fréquence particulière mais toutes les autres notes ont été définies comme ayant des fréquences égales à des fractions de la fréquence de « do ». Au cours de l'histoire, il y a eu plusieurs opinions sur les fréquences qui doivent constituer une gamme de douze notes.

Gamme pythagoricienne

Déjà les grecs de l'Antiquité se penchaient sur cette question.  Les mathématiciens de l'école de Pythagore étaient convaincus que tout peut être expliqué en n'utilisant que les nombres entiers ou bien des rapports entre eux. En fait, Pythagore ne reconnaissait pas l'existence d'autres nombres que les entiers et les rationnels. Fidèles à cette idée, les pythagoriciens sont arrivés à la solution suivante:

Leur raisonnement était comme suit. Il est naturel de vouloir que les notes « do »  espacées d'une octave se ressemblent. En termes mathématiques, ça veut dire que leurs fréquences doivent être des multiples entiers l'une de l'autre (de cette façon le deuxième « do »  coïncide avec le deuxième harmonique du « do »  de départ et donc on a l'impression que c'est la même note). Par exemple, si la fréquence du « do »  de départ (l'octave numéro un) est F, la fréquence du « do »  une octave plus haut (la deuxième octave) sera 2F. Notre raisonnement doit être le même quand on compare la deuxième octave et la troisième - nous obtiendrons que la fréquence du « do » de la troisième octave est deux fois 2F, donc égale à 4F. Le « do »  de la quatrième octave aura la fréquence 8F et ainsi de suite. Donc pour monter une octave on multiplie la fréquence par deux. 

Alors, le deuxième harmonique de « do »  est utilisé pour construire une octave. Le troisième harmonique, celui de la fréquence 3F, était aussi spécial pour les pythagoriciens. Comme la fréquence 3F dépasse l'intervalle d'une octave, ils l'ont divisée par deux pour la ramener dans l'octave numéro un et obtenu 3/2F. C'est la fréquence de la note «sol», la cinquième note de l'octave, et l'intervalle entre « do » et « sol » de la même octave (sept demi-tons) s'appelle quinte. De façon analogue à ce qu'on a fait pour l'octave - pour monter une quinte la fréquence est multipliée par 3/2 et pour descendre d'une quinte on divise la fréquence par 3/2 donc multiplie par 2/3. 

Seuls ces deux intervalles, octave et quinte, étaient considérés comme consonants par les pythagoriciens. Par conséquent, ces deux intervalles jouaient des rôles spéciaux dans la construction des autres notes de la gamme. Par exemple, ayant « do » et « sol » de l'octave un en main, montons d'une quinte en commençant par « sol ». Nous obtenons le « ré » de l'octave numéro deux et la fréquence correspondante sera 3/2×3/2F=9/4F. Ramenons-le dans l'octave un en divisant la fréquence par deux. Nous obtenons 9/8F. C'est la fréquence que les pythagoriciens ont associée à la note « ré » de l'octave un et ils ont procédé ainsi pour toutes les autres notes, en montant ou en descendant d'une quinte ou d'une octave. 

Un problème : le comma pythagoricien

Au cours de l'histoire plusieurs autres systèmes de fréquence ont été introduits, ils ressemblaient tous à ce que nous appellerons la gamme pythagoricienne. Cependant, ils ont tous un problème commun, ce qui a mis fin à leur utilisation avec l'apparition des instruments à clavier, tels que le clavecin et l'orgue. Le problème, dit le comma pythagoricien, est le suivant. 

Si on joue une mélodie simple qui est faite de notes à l'intérieur d'une octave ou deux, la gamme pythagoricienne ne pose pas de problème. Cependant un clavecin ou un orgue avait quatre octaves et un piano moderne en a sept. Regardons ce qui se passe si on monte de sept octaves en commençant par un « do » de l'octave numéro un qui a la fréquence notée F. 

Une octave contient douze demi-tons et une quinte en contient sept. Alors pour monter de sept octaves on peut aussi monter de douze quintes - ces deux démarches nous montent de 7×12=84 demi-tons. On sait qu'en montant de sept octaves on double la fréquence du départ sept fois de suite, alors on la multiplie par 2⁷ = 128. Tandis que monter de douze quintes correspond à la multiplication par 3/2 douze fois, donc par (3/2)¹²=531441/4096, ce qui est à peu près égal à 129,75. 

Voici un paradoxe - en montant de ces deux façons nous sommes supposés arriver à la même note, notamment le « do » de la huitième octave (la toute dernière clé sur le piano), mais nous avons obtenu deux fréquences différentes pour cette note:  128F et 129,75F. Notons que ces deux façons de calculer la fréquence du « do » de la huitième octave sont parfaitement valides et il n'y a pas de raison de préférer une et de rejeter l'autre. Pourtant, si on voulait construire un piano en suivant la gamme pythagoricienne, il fallait choisir entre les deux valeurs mentionnées, et par conséquent, un tel piano serait légèrement dissonant - soit les octaves soit les quintes ne seraient pas toutes équivalentes. 

À cause de cet effet, il était risqué de changer de tonalité pour une mélodie -  si une mélodie commence par un « do », il était difficile de la réécrire en commençant par une autre note - étant donné que les demi-tons n'étaient pas tous équivalents, une telle opération  modifierait la musique de façon inattendue. 

Le tempérament égal

C'était Jean-Sébastien Bach qui a décidé de rectifier la situation. En 1738, pour son célèbre «Clavier bien tempéré», il a changé les fréquences des notes de façon que la dissonance explicitée plus haut  soit moins importante. Le problème avec cette solution était que personne ne savait quelles fréquences exactes Bach utilisait parce qu'il accordait ses instruments à l'oreille. 

Évidemment, pour avoir un système viable il était nécessaire de formuler une règle que tous les musiciens et les fabricants d'instruments pouvaient appliquer. Une telle règle avait été trouvée cent cinquante ans avant le bon tempérament de Bach - en Chine! Un prince-mathématicien, Chou Tsaï Yu, était arrivé à une solution aussi mathématiquement parfaite que simple. 

Partons d'un « do » de l'octave un qui a la fréquence F. La fréquence du « do » de l'octave deux est 2F et il y a douze demi-tons entre eux. La solution de Chou Tsaï Yu nous semble maintenant évidente - il faut que tous les douze intervalles de demi-ton soient équivalents entre eux comme sont équivalents tous les intervalles d'une octave. 

Pour monter d'une octave nous multiplions la fréquence par deux. Supposons que pour monter d'un demi-ton nous multiplions la fréquence par un nombre R. Alors, la fréquence du « do # » sera R×F, la fréquence du « ré » sera R²×F et ainsi de suite jusqu'au «do» de l'octave suivante douze demi-tons plus haut pour qui nous obtenons R¹²×F comme fréquence. En même temps, nous savons que la fréquence de ce «do» est égale à 2F et donc nous obtenons l'équation R¹²=2 qui détermine la valeur de R comme étant la racine douzième de deux. Alors pour monter d'un demi-ton nous allons multiplier la fréquence par la racine douzième de deux, soit à peu près 1,05946 en système décimal! Si nous reprenons le « la » central du piano, à une fréquence de 440 Hz, on pourra donc calculer un «la dièse» (et un si bémol) à une fréquence de 466.16 Hz. Ainsi, tous les intervalles contenant le même nombre de demi-tons seront équivalents entre eux et il n'y aura plus de dissonance quelconque. 

Ce système, utilisé maintenant sous le nom de tempérament égal, a été présenté par Chou Tsaï Yu à l'empereur de Chine en 1595. En Europe cette solution n'a été connue que vers la fin du dix-septième siècle et n'a été adoptée que cent ans plus tard, à l'époque de Beethoven. 

Remarquons que les fréquences du tempérament égal sont numériquement assez proches des fréquences choisies par les pythagoriciens. Par exemple, dans la gamme pythagoricienne la note «sol» a la fréquence 1.5F où F est toujours la fréquence du « do » de base. Le tempérament égal prescrit plutôt 2^7/12×F = 1.49831F. Cependant, l'introduction du tempérament égal n'a pas fait l'unanimité. Les musiciens percevaient le nouvel accordement des instruments comme faux et refusaient de jouer de tels instruments. 

Professeure Vasilisa Shramchenko
Département de mathématiques

Référence : Les vérités de l'histoire, Sélection du Reader's Digest, 2010.