Termes quantiques

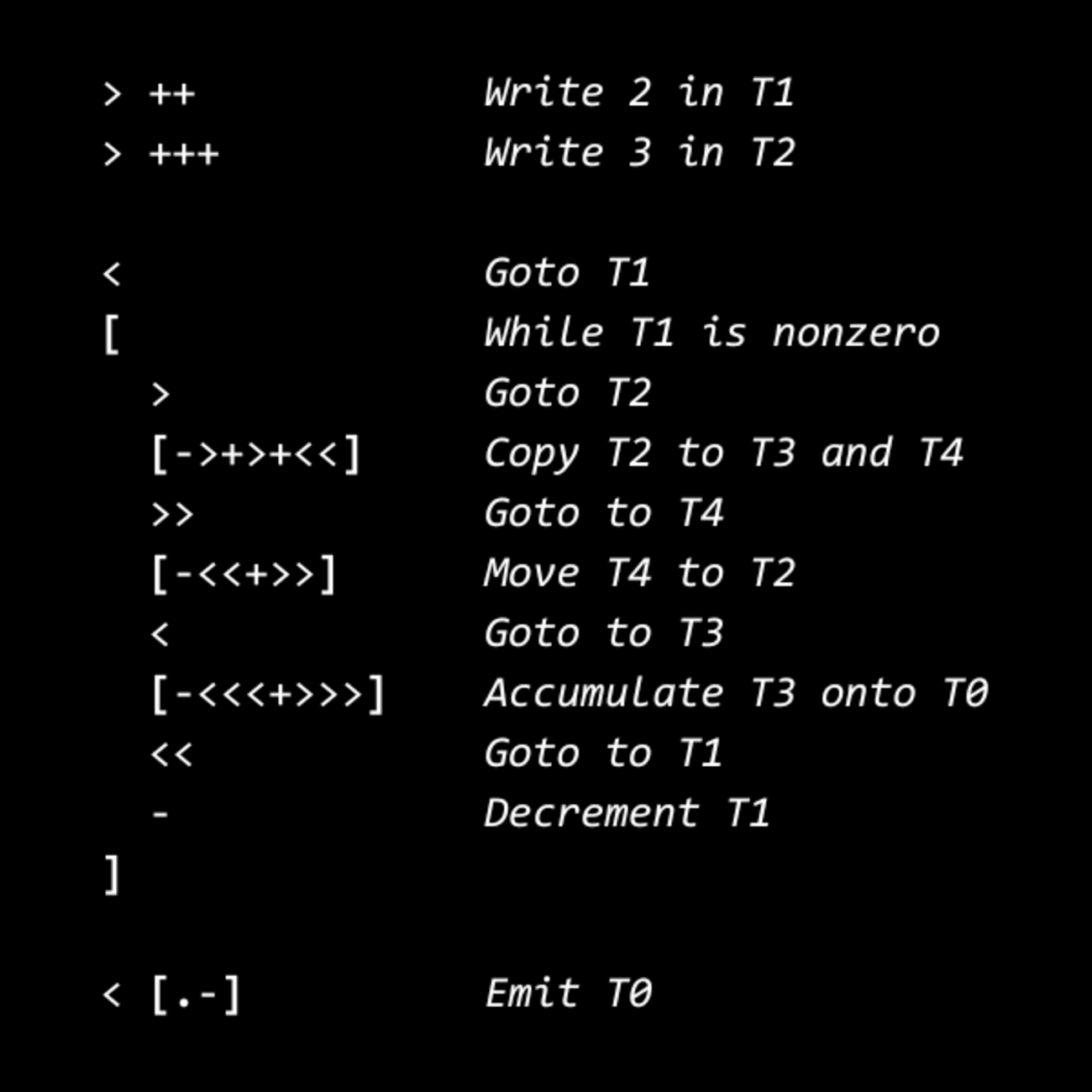
cover algorithme — Image: Algorithme représentant le calcul 2 x 3

Un algorithme est un enchaînement d’instructions qui permet de résoudre des problèmes. C’est comme une recette : il faut procéder aux étapes avec les bons ingrédients et dans le bon ordre afin d’obtenir le plat voulu.

Bien que les algorithmes soient fortement associés au domaine de l’informatique depuis la seconde moitié du 20e siècle, en réalité, l’humanité s’en sert depuis des millénaires. Les premiers exemples d’algorithmes proviennent de tablettes babyloniennes datant de jusqu’à 3000 ans av. J.-C. Celles-ci décrivent la résolution d’équations en incluant des exemples. Le terme « algorithme » vient quant à lui du nom d’un mathématicien du 9e siècle, Muhammad ibn Mūsā al’Khwārizmī, qui donne Algorithmi en traduction latine.

En informatique, les algorithmes donnent une suite d’instructions à l’ordinateur afin qu’il exécute une tâche spécifique. Par exemple, si on veut que l’ordinateur fasse un calcul, on doit écrire une série d’opérations élémentaires dans un langage informatique (Python, C++ ou JavaScript, par exemple). L’ordinateur exécute cet algorithme et renvoie le résultat. Les algorithmes s’appliquent à plusieurs domaines, comme l'intelligence artificielle et les mathématiques.

En informatique quantique, les algorithmes sont programmés avec les ordinateurs quantiques qui exploitent plusieurs propriétés quantiques, comme la superposition d’états et l’interférence. Les ordinateurs quantiques et classiques ne sont pas équivalents : leur approche de programmation ainsi que leurs usages diffèrent. Les ordinateurs classiques sont très polyvalents et peuvent exécuter des tâches variées telles que la consultation de courriels ou le visionnement de vidéos. Les ordinateurs quantiques ont le potentiel d’être plus puissants, spécifiquement pour la résolution de tâches complexes comprenant beaucoup de données, de variables ou d’étapes, comme les questions d’optimisation. Les algorithmes quantiques solutionneraient ce type de problèmes très rapidement, alors qu’un algorithme classique ne pourrait pas toujours les résoudre en un temps raisonnable.

Écoutez des membres de la communauté de l'IQ prononcer ce terme dans leur langue maternelle :

Imaginez qu’on vous enferme dans une bibliothèque dont le verrou s’ouvre seulement si vous prononcez une phrase précise tirée de l’un des livres. Quel cauchemar, il vous faudrait des années pour feuilleter chaque ligne de chaque livre et retrouver la bonne phrase! Heureusement, au détour d’une étagère, vous trouvez un ordinateur quantique : vous êtes donc sauvé, puisque vous pourrez recourir à l’algorithme de Grover.

Cet algorithme quantique, conçu en 1996 par Lov Grover, permet de retrouver une entrée spécifique dans une base de données non triée. Tandis qu’un algorithme classique doit tester les entrées l’une après l’autre, l’algorithme de Grover exploite les phénomènes de superposition d’états, d’intrication et d’interférence afin de tester plusieurs entrées à la fois selon le critère souhaité.

Dans la mise en scène de la bibliothèque, l’ordinateur quantique feuillèterait donc plusieurs phrases de plusieurs livres en même temps. Plus exactement, l’algorithme de Grover retrouve l’entrée recherchée en un nombre de vérifications proportionnel à la racine carrée du nombre total d'éléments. Ainsi, il n’a besoin que de mille vérifications pour retrouver le bon élément parmi un million d’entrées, ce qui vous permet de vous échapper plus rapidement.

Bien entendu, il s’agit d’un exemple fictif, d’autant plus que nous ne disposons pas encore d’un ordinateur quantique assez performant pour exécuter un tel algorithme quantique. Néanmoins, l’algorithme de Grover est relativement facile à comprendre et permet de voir le potentiel de l’informatique quantique.

Écoutez des membres de la communauté de l'IQ prononcer ce terme dans leur langue maternelle :

Petit défi mathématique : quels chiffres premiers donnent 35 en les multipliant ensemble? Vous avez certainement trouvé en quelques secondes que c’est 5 et 7. Qu’en est-il des deux chiffres premiers donnant 41828363? Ça vous prendrait assurément un bon moment d’essais et d’erreurs pour enfin arriver à identifier 5869 et 7127.

Ne vous en faites pas : même les superordinateurs effectuent difficilement ce type de tâche nommée factorisation. C’est même sur cette difficulté de calcul que repose l’une des façons de crypter les plus courantes, le chiffrement RSA, qui protège des informations bancaires, médicales, gouvernementales, etc. Lorsqu’une clé RSA a une longueur de 2048 bits, un ordinateur classique peut prendre des centaines d’années avant d’arriver à la factoriser, voire plus, alors on considère que les informations confidentielles sont bien protégées… Pour le moment! Car les ordinateurs quantiques pourraient changer la donne, avec l’algorithme de Shor.

En effet, en 1994, le mathématicien Peter Shor a proposé un algorithme quantique capable de factoriser beaucoup plus rapidement. Une clé RSA de 2048 bits pourrait être craquée en seulement 8 heures, avec un ordinateur quantique de 20 millions de qubits. Cet exploit, on le doit à la superposition d’états qui permet en quelque sorte aux qubits de traiter en même temps plusieurs informations superposées.

Mais si cet algorithme existe déjà, comment se fait-il que le chiffrement RSA soit toujours en vigueur? C’est que nous sommes encore loin d’avoir ce fameux ordinateur à 20 millions de qubits. Les chercheurs en quantique continuent de repousser la limite, mais présentement, il est difficile de disposer de plus d’une poignée de qubits, et leur performance reste imparfaite. Et si ça ne suffit pas à vous rassurer, sachez qu’en plus, des algorithmes adaptés pour résister à la puissance quantique de calcul – qui peuvent fonctionner avec des ordinateurs quantiques ou classiques – sont déjà en cours de développement et d'implantation.

Écoutez des membres de la communauté de l'IQ prononcer ce terme dans leur langue maternelle :

Qu’est qu’un atome, où ça se trouve, ça ressemble à quoi de l’intérieur et peut-on l’observer?

L’idée que la matière soit composée de perles minuscules et invisibles était déjà défendue par des philosophes en 3300 av. J.-C. Grâce au microscope, qui nous a offert un voyage au centre de la matière, l’observation d’un atome fut possible vers le milieu du XXe siècle.

L’atome est une particule de la matière et constitue l’unité de base d’une molécule. Tout ce qui nous entoure à l’échelle microscopique est constitué d’atomes. Les caractéristiques de ces atomes ainsi que leur arrangement tridimensionnel déterminent les propriétés de la matière avec laquelle on interagit au quotidien.

La masse de l’atome est concentrée dans son noyau, qui est formé de deux types de particules subatomiques: les protons qui portent une charge électrique élémentaire positive et les neutrons qui sont des particules neutres.

Le noyau est entouré par un nuage électronique où les électrons, particules subatomiques chargées négativement, se distribuent sur des couches caractérisées par un niveau d’énergie. L’énergie d’un électron est ainsi quantifiée. Un électron se comporte parfois comme une particule et parfois comme une onde, révélant ainsi sa nature quantique. C’est ce que l’on nomme la dualité onde-corpuscule.

L’étude de la matière au niveau atomique a contribué au développement de la physique et de la mécanique quantique.

Écoutez des membres de la communauté de l'IQ prononcer ce terme dans leur langue maternelle :

On qualifie fréquemment la mécanique quantique d’« étrange » et, que cela vous rassure, les personnes à l'origine de cette théorie n’en étaient pas moins inconfortables avec certaines de ses implications!

En 1935, Albert Einstein, Boris Podolsky et Nathan Rosen publient un article (EPR) qui tente de démontrer que la théorie de la mécanique quantique est incomplète en utilisant une expérience de pensée. Ce papier fera grand bruit car il aborde la question fondamentale de ce qu’est la « réalité ».

Quelques mois plus tard, en écho à l’article EPR, le physicien Erwin Schrödinger décrit l’expérience de pensée suivante : Une substance radioactive se trouve dans une boîte fermée dans laquelle on place également un chat ainsi qu’une fiole de cyanure. La substance radioactive a 50% des chances de se désintégrer sur une période de 1 heure; elle est donc à la fois désintégrée (état M) et non-désintégrée (état V): en superposition d’états! Ce n’est qu’en mesurant la substance qu’on forcera le système à être soit dans l’état M, soit dans l’état V. Cependant, un mécanisme fait en sorte que si la substance se désintègre, la fiole de cyanure sera brisée et le chat … mort. Ainsi, avant d’ouvrir la boîte, le chat de Schrödinger est à la fois mort et vivant!

Cette expérience de pensée met en lumière le rôle fondamental – et pas toujours clair – de la mesure en mécanique quantique. Encore de nos jours, il existe plusieurs interprétations qui tentent de donner un sens à cette théorie. Une chose est certaine cependant : pour l’écriture de ce terme quantique, aucune expérience n’a été menée sur des animaux!

Écoutez des membres de la communauté de l'IQ prononcer ce terme dans leur langue maternelle :

Cover curate supra — Image: Dmitry Veselov/Shutterstock

Les cuprates sont une famille de matériaux supraconducteurs, c-à-d qui conduisent parfaitement l’électricité sans perte d’énergie. Comme leur nom l’indique, les cuprates sont des céramiques synthétiques à base d’oxyde de cuivre. Ces céramiques sont obtenues en réduisant en poudre les composés solides comme de l’oxyde puis en les mélangeant et en les recuisant selon des paramètres spécifiques.

Comme la plupart des supraconducteurs, les propriétés des cuprates se révèlent sous des conditions spéciales, notamment à de très basses températures ou encore à des niveaux élevés de pression. La température à laquelle un matériau devient supraconducteur se nomme la température critique, qui peut varier en fonction de la pression. En général, la température critique des supraconducteurs à pression atmosphérique est extrêmement basse, ce qui complique leur utilisation. Pour certains matériaux, il est possible d’augmenter la température critique en les soumettant à de très fortes pressions.

Ce sont Johannes Georg Bednorz et Karl Alexander Müller qui firent la découverte du premier cuprate supraconducteur en 1986. Ils observèrent qu’un composé à base de lanthane, de baryum et d’oxyde de cuivre devenaient supraconducteurs autour de 30 kelvins ou -243˚ C à pression atmosphérique!

Depuis cette découverte, les recherches et percées se sont enchaînées afin de trouver des nouveaux cuprates aux températures critiques plus élevées. En 1993, on a abouti à la plus haute température critique à pression atmosphérique jamais mesurée dans un cuprate à base de mercure avec une température critique avoisinant les 130 kelvins, soit de -140˚ C.

Ultimement, on cherche un supraconducteur avec une température critique qui se rapproche de la température ambiante et ce, à pression atmosphérique. Cela permettrait non seulement de transporter l’électricité sans perte énergétique, mais également d’avoir des applications comme des ordinateurs quantiques supraconducteurs. La découverte d’un tel matériau serait une révolution technologique importante!

Écoutez des membres de la communauté de l'IQ prononcer ce terme dans leur langue maternelle :

Imaginez une calculatrice très fragile qui « oublie » les premiers chiffres entrés avant même que vous n’appuyiez sur le « = ». Pas très pratique, n’est-ce pas? Pourtant, il s’agit d’une difficulté majeure rencontrée par les ordinateurs quantiques encore à ce jour: la décohérence.

Définie comme la perte de cohérence quantique, cette décohérence survient parce que les états quantiques sur lesquels reposent les calculs (par exemple un état de superposition) sont très fragiles et persistent à peine quelques fractions de seconde dans tout environnement qui n’est pas parfaitement isolé. Même dans un ordinateur quantique qui est conçu pour être hautement isolé, certaines perturbations (onde électromagnétique, vibration, chaleur…) arrivent à s’infiltrer. Elles peuvent alors affecter l’état des qubits. En plus de la décohérence, des erreurs peuvent survenir lors de la programmation ou de la mesure.

Rappelons néanmoins que lorsque les avancées technologiques permettront d’augmenter le temps de cohérence et de réduire les autres sources d’erreurs, les ordinateurs quantiques seront capables de prouesses inaccessibles aux ordinateurs classiques.

Par ailleurs, le phénomène de la décohérence ne se limite pas qu’aux ordinateurs quantiques: elle survient avec tout minuscule objet (électron, photon, etc.) capable d’être en superposition d’états.

De nombreux physiciens croient que la décohérence expliquerait pourquoi les phénomènes quantiques qui ne sont pas observables dans notre quotidien: il y a tellement d’interactions biologiques et environnementales en tout temps autour de nous qu’aucun effet quantique ne dure assez longtemps pour être observé ou pour avoir un effet à notre échelle.

Écoutez des membres de la communauté de l'IQ prononcer ce terme dans leur langue maternelle :

Cover dualité onde — Image: Wikimedia commons

La nature de la lumière a été l’objet d’un long débat. Pourquoi la nature de la lumière était controversée? Qu’est-ce qu’on entend par une nature duale?

Au 17e siècle, deux théories s’affrontent pour expliquer la nature de la lumière. Christian Huygens soutient qu’elle a un comportement ondulatoire, tandis qu’Isaac Newton stipule qu’elle est une particule. Vu la notoriété de Newton à l’époque, la seconde théorie est dominante, malgré ses quelques limitations.

Au 18e siècle, Thomas Young reprend la théorie de Huygens et crée l’expérience maintenant connue sous le nom des fentes de Young. Celle-ci a permis de prouver la nature ondulatoire de la lumière.

Finalement, au 20e siècle, Albert Einstein revient avec la théorie corpusculaire de la lumière, qui fut plus tard démontrée expérimentalement par Arthur Compton en 1923. Ainsi, on a pu prouver que la lumière possède à la fois des propriétés des particules et des ondes! Une particule de lumière se nomme un photon.

D’ailleurs, en répétant l’expérience des fentes de Young mais avec un canon propulsant des photons uniques, c’est-à-dire un à la fois, on peut observer ces deux natures de la lumière, qu’on appelle en physique la dualité onde-corpuscule. Cette expérience permet d’observer une figure d’interférence sur un écran, témoignant de la nature ondulatoire de la lumière, ainsi que les particules de lumière qui sont détectées sur un écran une à la fois.

Il n’y a pas que la lumière qui possède cette dualité. Les particules élémentaires, comme les électrons, les protons, et bien d’autres répondent aussi à ce principe. On qualifie alors ces particules élémentaires de systèmes quantiques.

En mécanique quantique, on explique la figure d’interférence obtenue dans l’expérience des fentes de Young en décrivant un photon à l’aide d’une fonction d’onde. Cette fonction d’onde associée à un système quantique représente la probabilité de trouver la particule à un certain endroit. Cela signifie qu’on a besoin d’utiliser à la fois les notions des ondes et des particules pour étudier un système quantique. C'est pourquoi on dit souvent que la dualité onde-corpuscule est au cœur de la mécanique quantique!

Écoutez des membres de la communauté de l'IQ prononcer ce terme dans leur langue maternelle :

À la manière des gracieuses nuées d’oiseaux ou des vifs bancs de poissons, une grande quantité de particules peuvent adopter des comportements collectifs. En quantique, on appelle « émergence » l’apparition de propriétés à l’échelle macroscopique à partir d’interactions locales.

Ce phénomène explique par exemple la supraconductivité, car la résistance électrique qui devient nulle découle d’une interaction spéciale entre les électrons. En effet, ceux-ci forment des « paires de Cooper », soit des paires d’électrons qui interagissent entre elles. Chaque électron n’agit alors plus indépendamment, mais plutôt comme une partie d’un tout cohérent. Autrement dit, la résistance nulle n’existe pas pour un électron isolé : elle ne survient qu’avec le comportement collectif des paires de Cooper dans un matériau supraconducteur suffisamment refroidi.

Un autre exemple d’émergence en quantique inclut les quasiparticules, c’est-à-dire l’excitation collective d’un ensemble de particules, qui se comporte alors comme une seule entité sous certaines conditions. Par exemple, le phonon est la quasiparticule qui décrit l’excitation quantifiée d’un mouvement mécanique tel que la vibration des atomes dans un cristal.

Même s’il est charmant de s’imaginer les particules valsant comme des oiseaux à l’échelle subatomique, il faut tout de même noter que les mécanismes derrière ces comportements collectifs diffèrent. Dans un cas, le phénomène s’explique par les réflexes des animaux face à leur environnement et aux mouvements de leurs voisins immédiats, et dans l’autre, par les lois de la physique à l’échelle quantique.

N’en demeure pas moins que, dans la nature comme en quantique, l’ensemble peut s’avérer plus fascinant et complexe que la somme de ses parties !

Qu’ont en commun la lumière du soleil, un aliment ou une vague à la surface de l’océan ? Bien peu à première vue, mais on peut avancer sans se tromper que ce sont des entités qui partagent la caractéristique de contenir de l’énergie. En fait, cette liste aurait pu être beaucoup plus longue puisque tout contient de l’énergie, que l’on pourrait définir comme une quantité qui demeure constante pour un système physique isolé.

À la fin du 19e siècle, les physiciens ne peuvent expliquer le spectre du rayonnement thermique du corps noir, soit un objet qui absorbe toute la lumière qu’il reçoit. Cet échec de la physique de l’époque est nommé la « catastrophe ultraviolette ». C’est Max Planck qui, en 1900, a résolu ce problème en introduisant le principe de quantification de l'énergie. Selon ce principe, l'énergie ne peut prendre que des valeurs discrètes consistant en des multiples entiers d’un quanta d’énergie défini par la fréquence du rayonnement multiplié par la constante de Planck, h. La quantification de l’énergie en quanta, a donné naissance au terme quantique.

La quantification de l'énergie nous informe également comment les électrons d'un atome sont disposés en différents niveaux d'énergie. Nous pouvons ainsi déterminer la quantité d'énergie qui doit être transmise à un atome pour modifier sa configuration électronique. C’est ainsi qu’on peut développer des matériaux optimisés pour capter l’énergie du soleil ou encore pour émettre de la lumière d’une longueur d’onde bien précise.

Dans le domaine de l’informatique quantique, la quantification d'énergie joue un rôle essentiel car elle nous permet de construire des qubits! Par exemple, les qubits supraconducteurs possèdent un spectre d'énergie ressemblant à celui d'un atome et c'est pourquoi on les appelle parfois des atomes artificiels. Grâce aux lois de la mécanique quantique, nous sommes capables d'isoler les deux premiers niveaux d'énergie d’un tel système pour leur attribuer les valeurs 0 et 1. On obtient alors un bit d’information avec des propriétés quantiques : un qubit.

Écoutez des membres de la communauté de l'IQ prononcer ce terme dans leur langue maternelle :

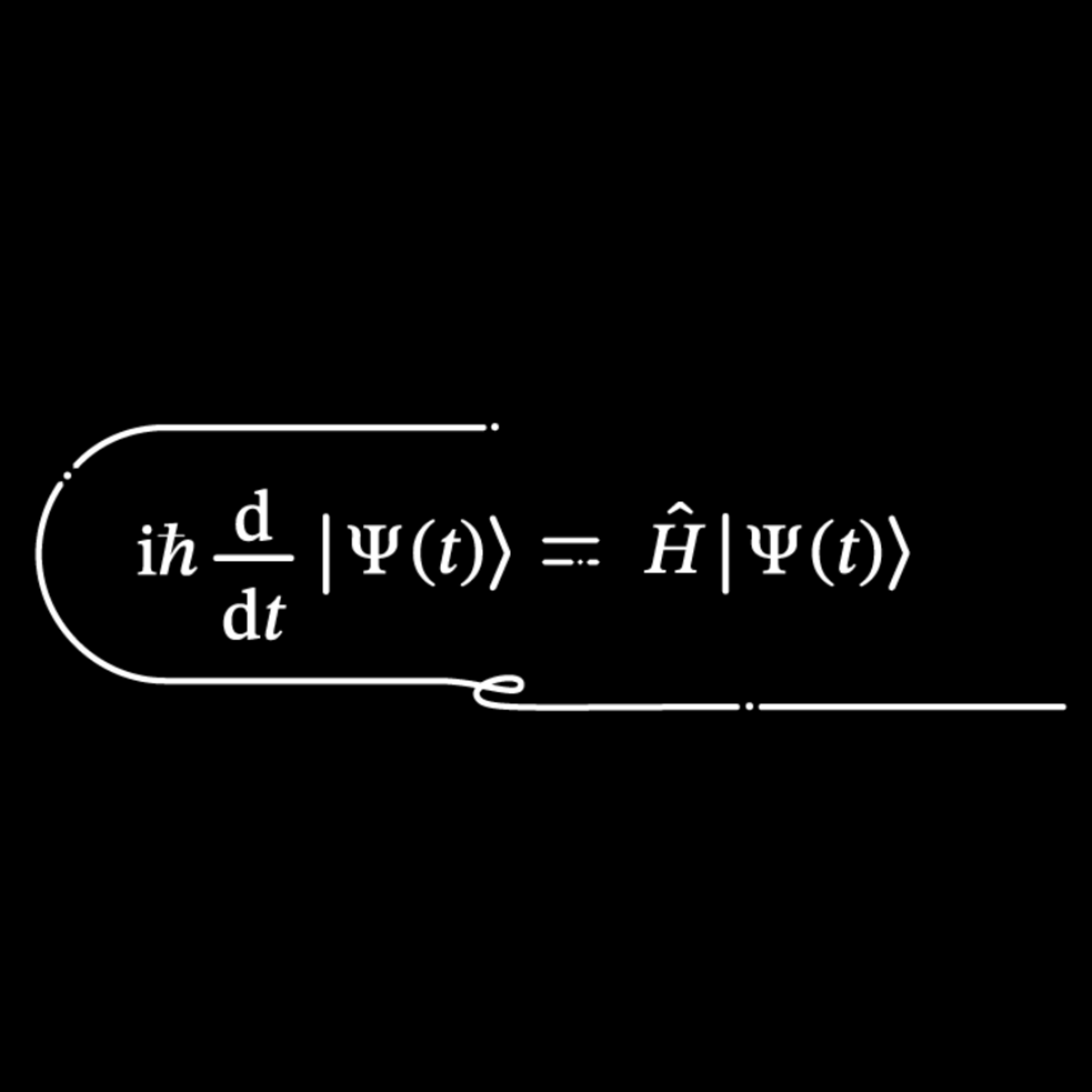
Équation de Schrödinger Institut quantique

Ce n’est pas tout le monde qui, après avoir reçu une pomme sur la tête, se mettrait passionnément à chercher les règles régissant le mouvement des objets. Mais heureusement pour nous, c’est ce qui serait arrivé à Newton, selon la légende. Ses travaux ont permis une meilleure compréhension physique et mathématique du mouvement des objets tels que nous les percevons. Par exemple, on peut prévoir la position exacte des objets en mouvement au cours du temps qui passe. Par contre, il y a une limite : lorsqu’on s’intéresse aux objets de taille atomique et subatomique, les règles dites « classiques » ne fonctionnent plus, comme l’illustre le principe d’incertitude.

C’est le physicien autrichien Erwin Schrödinger qui propose en 1925 une solution pour le monde quantique, avec la fameuse équation portant son nom. Celle-ci permet de calculer l’évolution de l’état d’un objet quantique, comme les photons ou les électrons, afin de représenter mathématiquement son état quantique dans le temps et l’espace.

Pour mieux s’imaginer ce que cela signifie, on peut faire un parallèle avec la 2^e loi de Newton en physique classique, en prenant par exemple un système composé d’un poids suspendu à un ressort. Lorsque le poids oscille, on peut recourir à l’équation de mouvement afin de calculer la position exacte du poids par rapport au temps.

C’est similaire à ce que peut faire l’équation de Schrödinger, sauf que dans ce cas, l’équation sert à décrire l’évolution d’un état quantique. Par exemple, on peut chercher à décrire le spin d’un électron ou la phase d’un qubit. Le résultat de l’équation de Schrödinger donne alors l’amplitude des probabilités pour le système d’être mesuré dans un état ou un autre.

Et tout ça sans avoir eu besoin de recevoir une pomme sur le crâne!

Écoutez des membres de la communauté de l'IQ prononcer ce terme dans leur langue maternelle :

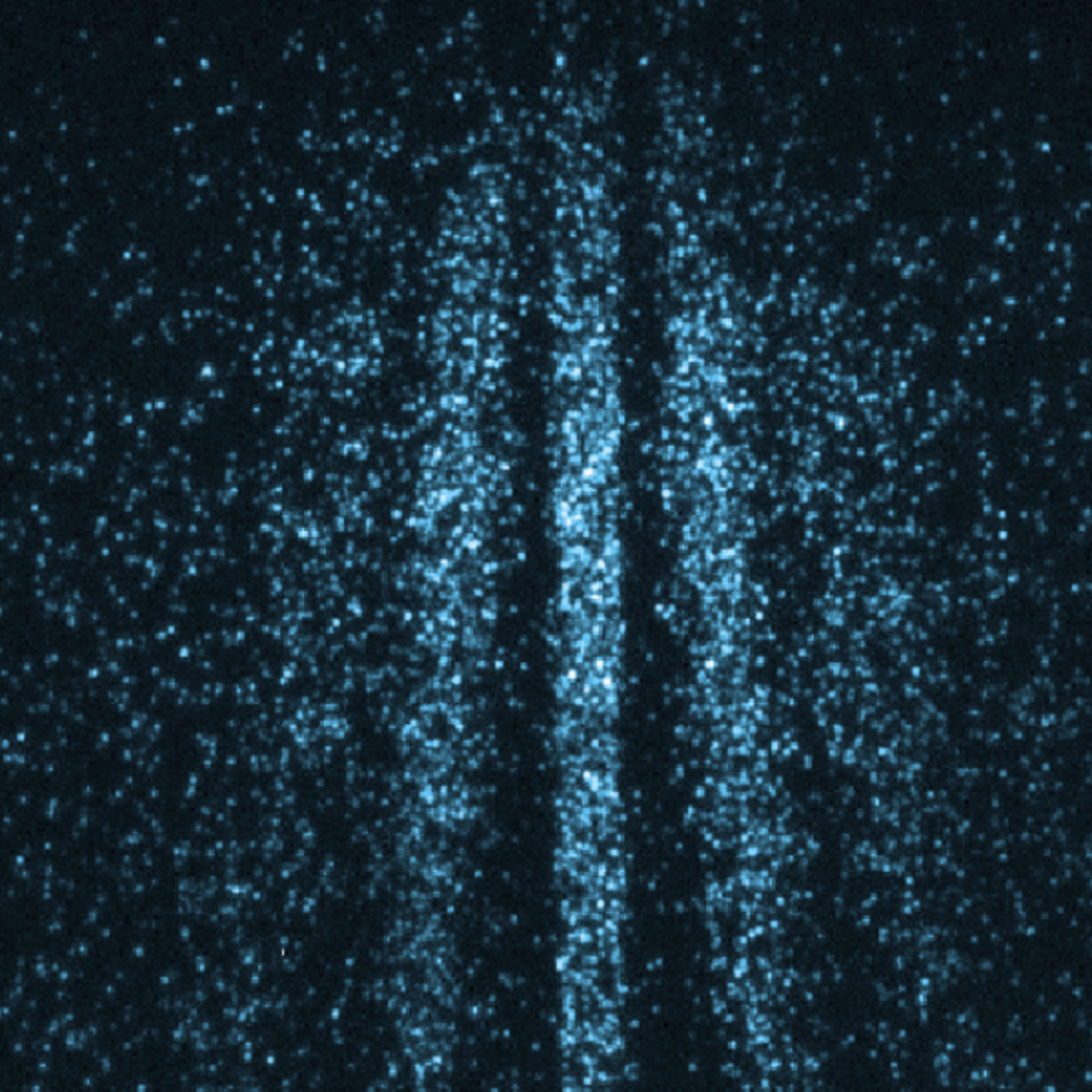
cover fentes young — Image: Wikimedia commons

L'expérience des Fentes de Young, réalisée en 1801 par Thomas Young, démontre la dualité onde-corpuscule de la lumière. Imaginons un canon projetant des photons, les particules de la lumière, à travers deux fentes vers un écran noir. Si ces photons étaient des balles de peinture, on s'attendrait à la formation de deux bandes de couleur alignées avec les fentes. Mais est-ce réellement ce qui se passe?

Quand deux ondes se rencontrent, elles interfèrent, à la manière de deux vagues qui se croisent. Si deux sommets collisionnent, ils s'additionnent, mais si un sommet rencontre un creux, ils s'annulent. Et justement, si l’on envoie plusieurs photons un par un, étrangement, un motif d'interférence se forme, comme si un photon pouvait interférer avec lui-même. Pourtant, si un photon était une particule, et non une onde, il devrait passer par une des deux fentes, n'est-ce pas?

De plus, lorsque les physiciens ont ajouté un détecteur aux fentes afin d’observer par quel chemin est passé chaque photon, ces derniers ont soudainement commencé à se comporter comme des particules, produisant deux bandes de couleurs! Ceci est le paradoxe de l’observateur : selon la façon dont une particule quantique est mesurée, son comportement change.

Lorsque l'on mesure la position d'un photon, on contraint sa position à être définie, et il acquiert alors les propriétés d'une particule. En revanche, en absence d’interaction avec un appareil de mesure, le photon peut se propager par les deux fentes en même temps, comme le ferait une onde, d’où la possibilité qu’il puisse interférer avec lui-même! Ainsi, l'expérience des fentes de Young illustre la nature étrange et dualiste de la lumière.

Écoutez des membres de la communauté de l'IQ prononcer ce terme dans leur langue maternelle :

Connaissez-vous la blague d’Heisenberg et Schrödinger qui voyagent ensemble en voiture ? Ils se font arrêter par la police qui leur demande « Vous avez vu à combien vous rouliez ? » En panique, les physiciens répondent « Non, non ! Ne nous le dites surtout pas ! » mais la police les ignore et enchaine « Vous rouliez à 142 km/h !!! » Découragés, les physiciens s’exclament « Formidable… nous voilà maintenant perdus ! »

Pour comprendre cette blague en apparence absurde, il faut remonter à 1927, lorsque le physicien allemand Werner Heisenberg formulait pour la première fois son principe d'incertitude, également connu sous le nom de principe d'indétermination. Ce principe soutient que certaines paires de propriétés concernant un objet quantique ne peuvent pas être connues simultanément avec une précision infinie. L’exemple le plus connu est la paire position et quantité de mouvement (momentum) : pour un temps donné, plus la précision sur la quantité de mouvement est grande, moins celle sur la position le sera. Ainsi, mesurer finement la quantité de mouvement d'une particule revient à perdre sa trace... d’où la réaction agacée de nos deux physiciens lorsqu’ils ont appris leur vitesse !

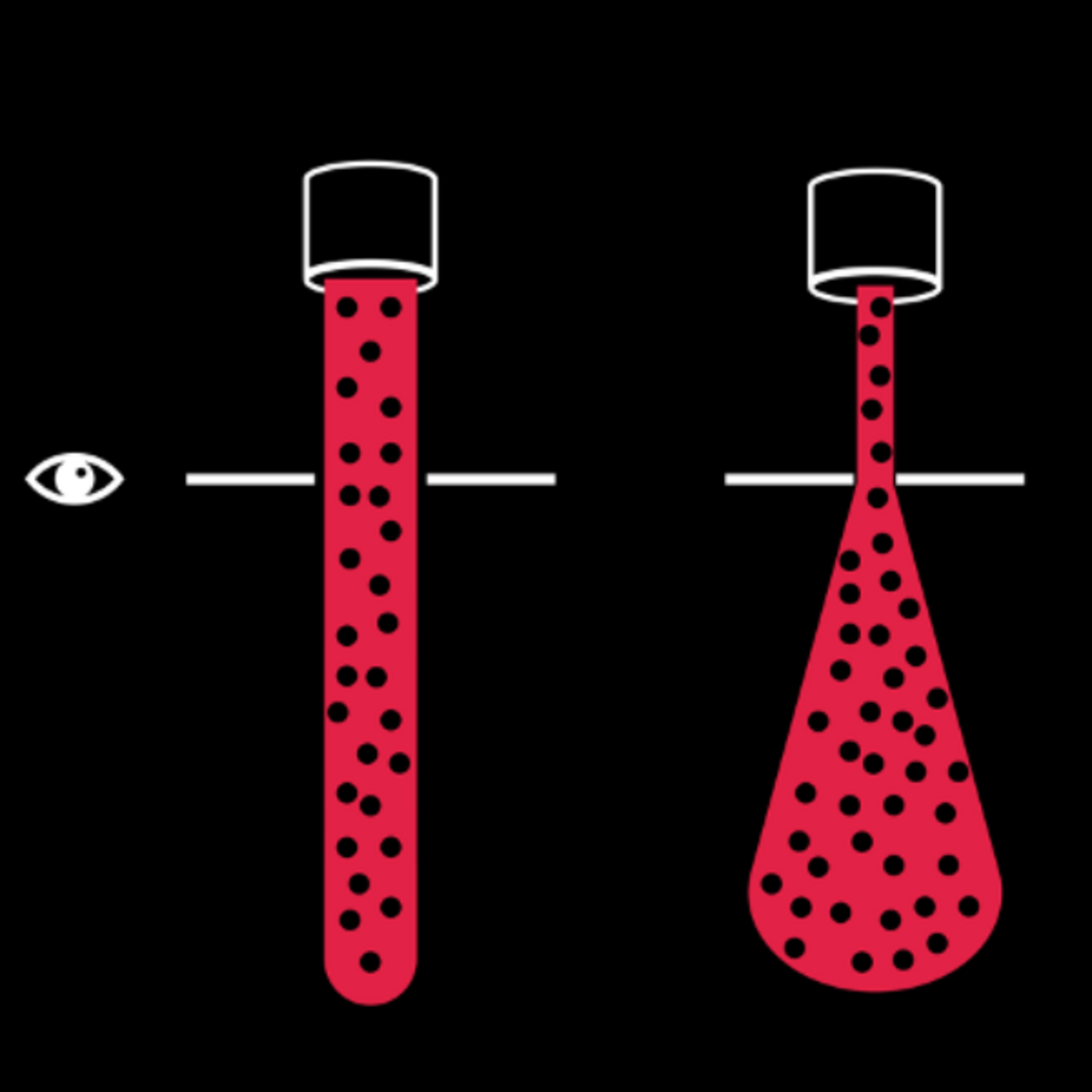
De même, si on fait passer un faisceau de particules à travers une fente très fine, on connaît avec une grande exactitude sa position à cet endroit. Il en résulte un élargissement du faisceau en sortie de la fente, car la quantité de mouvement des particules devient incertaine et elles se mettent à partir dans tous les sens.

En mécanique quantique, ce qui entoure la mesure est contre-intuitif, y compris le principe d’incertitude et comment la mesure influence l’état d’un objet physique. Il existe d’autres paires de propriétés concernées par le principe d’incertitude, comme l’énergie et le temps.

À noter que cet effet se distingue de l’incertitude en physique classique, où le terme réfère seulement aux limites technologiques de l’appareil de mesure.

Écoutez des membres de la communauté de l'IQ prononcer ce terme dans leur langue maternelle :

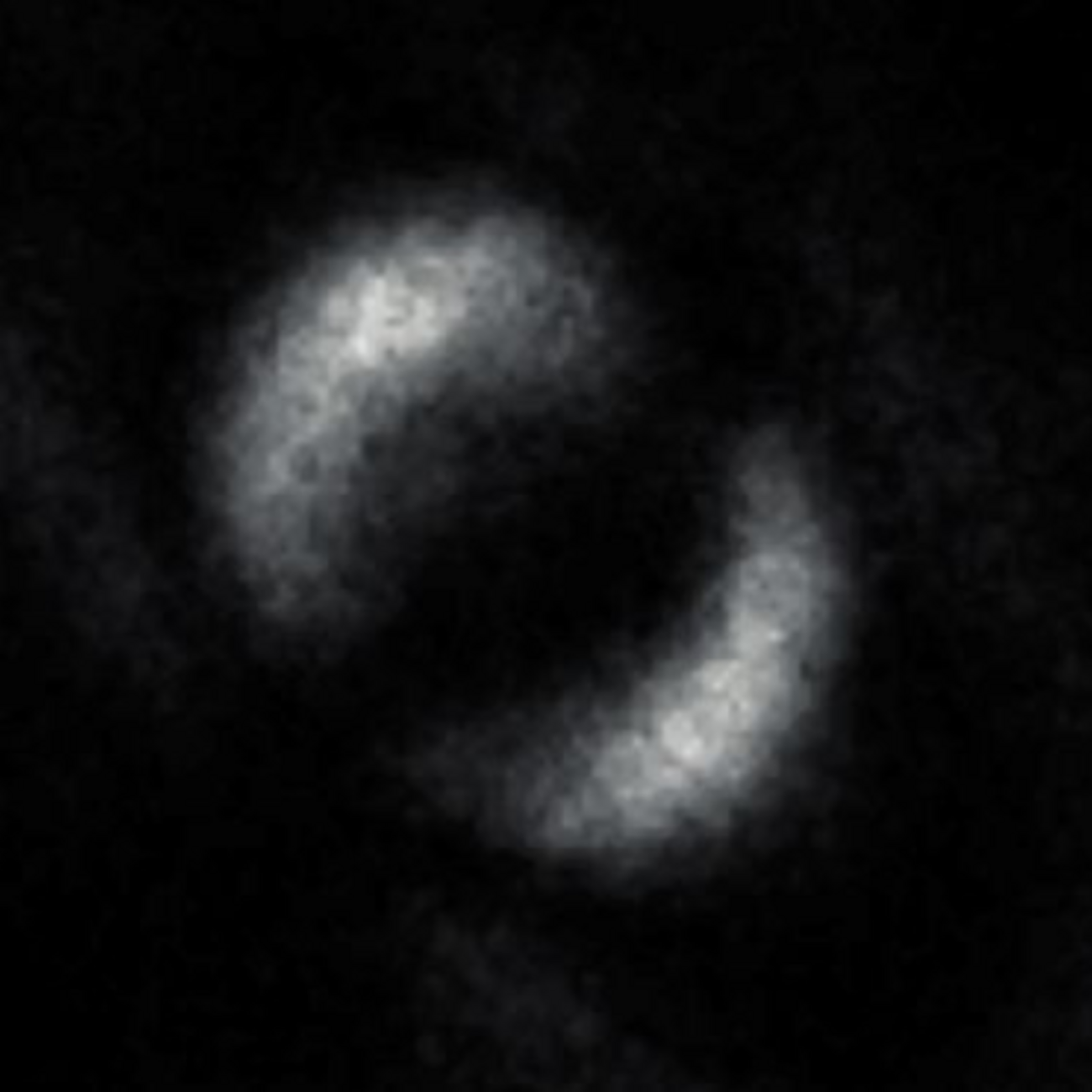
Cover intrication — Image: Université de Glasgow

Lorsque deux particules sont intriquées, la mesure d’une des particules va instantanément influencer l’état de l’autre particule de façon identique peu importe la distance qui les sépare dans l'univers. C'est ce qu'on appelle l'intrication ou l'enchevêtrement.

L’intrication est l’une des propriétés les plus étranges de la mécanique quantique, et fut longtemps contestée par la communauté scientifique. Le père de la mécanique quantique Albert Einstein lui-même n'y croyait pas et caractérisait le phénomène d'action fantôme à distance.

L'intrication a des conséquences sur le concept de localité en physique et le principe selon lequel rien ne voyage plus rapidement que la vitesse de la lumière.

Ce caractère contre-intuitif d'états intriqués fut abordé par Albert Einstein, Boris Podolsky et Nathan Rosen en 1935 dans un article pour démontrer les limites théoriques de la mécanique quantique. Le paradoxe EPR porte d'ailleurs les initiales des noms de famille des trois physiciens.

En 1982, Alain Aspect et Philippe Grangier menèrent la première expérience qui démontra de manière incontestable le phénomène d'intrication quantique. Depuis, plusieurs expériences ont validé l'intrication sur des distances de milliers de kilomètres.

En 2019, une équipe de physiciens de l’université de Glasgow a réussi à photographier pour la première fois l'intrication quantique entre deux particules.

L'intrication est essentielle à l'ordinateur quantique qui promet de grandement surpasser la capacité de calcul des ordinateurs classiques pour certains types de problèmes.

Écoutez des membres de la communauté de l'IQ prononcer ce terme dans leur langue maternelle :

Si vous demandez à une personne qui étudie la physique ce qu'est un matériau quantique, elle prendra un malin plaisir à vous répondre : tout! Pour l'utilité d'une telle définition, on repassera! Pourtant, cette plaisanterie cache une certaine vérité, car la physique quantique étudie l'énergie et les comportements de la matière à très petite échelle, typiquement à l’échelle des atomes et des particules subatomiques... Autrement dit, on peut effectivement observer des phénomènes quantiques dans pratiquement n'importe quoi, du moment qu’on s'y intéresse à la bonne échelle dans les bonnes conditions expérimentales.

C'est bien beau dit comme ça, mais concrètement, quels sont donc les matériaux sur lesquels les équipes de recherche en quantique restent penchées pendant des années dans leur laboratoire?

Les liquides de spins quantiques, les supraconducteurs ou encore les matériaux à deux dimensions comme le graphène en sont quelques exemples. Ces différents sujets d’étude ont une chose en commun : la physique classique ne peut pas expliquer leurs propriétés, il faut absolument recourir aux lois de la mécanique quantique pour y arriver.

Souvent, les électrons dans les matériaux quantiques ont des comportements inhabituels où ils interagissent fortement ou sont confinés à des dimensions spatiales réduites. Par ailleurs, on y retrouve souvent des quasi-particules, c’est-à-dire des excitations collectives qui amènent un nouveau comportement de la matière.

Les matériaux quantiques sont étudiés pour leurs applications potentielles en informatique quantique, en électronique ou encore en photonique, en autres. De plus, en les étudiant, les physiciens peuvent tirer des connaissances servant à mieux comprendre les phénomènes quantiques d’un point de vue fondamental.

Bref, derrière les blagues de physique, on retrouve généralement des vérités bien intrigantes!

Écoutez des membres de la communauté de l'IQ prononcer ce terme dans leur langue maternelle :

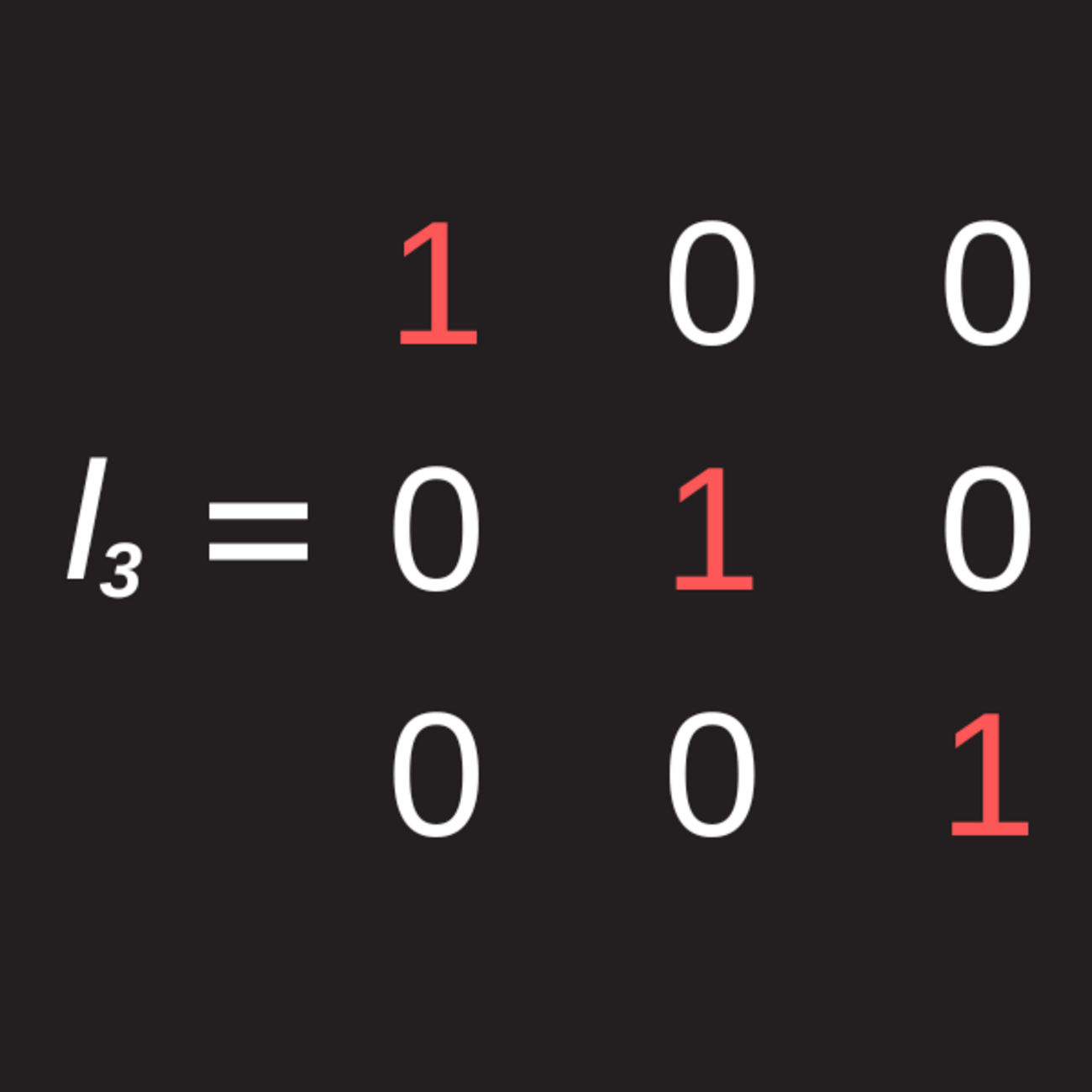
Ça ressemble à quoi une matrice et comment ça s’est introduit dans le domaine de la physique quantique?

En mathématiques, une matrice est un tableau de nombres ou de caractères utilisé pour étudier des phénomènes linéaires. Les matrices sont très utiles dans la résolution des systèmes à plusieurs équations et variables. L’utilisation des matrices en tant que tableaux de nombres date du IIe siècle avant J-C.

Une matrice formée de m lignes et n colonnes est dite de dimension m x n. Par exemple une matrice de nombres 1 x 1 est formée par un seul nombre. Une matrice de dimension 3 × 3 dont les seuls éléments non-nuls sont les éléments sur la diagonale, et que ceux-ci sont tous des 1 se nomme matrice identité (voir image ci-bas).

En 1925, les trois physiciens allemands Werner Heisenberg, Max Born et Pascual Jordan commencent à utiliser les matrices pour interpréter les propriétés physiques des particules évoluant dans le temps. Le langage mathématique des matrices n’était pas familier aux physiciens de cette époque. Ainsi ils introduisent leur formulation de la mécanique quantique, appelée la mécanique matricielle.

Les matrices sont alors utilisées un peu partout en physique quantique. On cite comme exemples les matrices de Pauli utilisées pour représenter le spin d’une particule ou encore la matrice densité qui permet de décrire un système quantique dont on ne connait pas précisément l’état.

Heisenberg fut lauréat du prix Nobel en 1932 pour la création de la mécanique quantique alors que Born le fut en 1954 pour l’interprétation statistique de la mécanique quantique.

De nos jours, la mécanique matricielle est considérée comme une description précise, rigoureuse et complète de la mécanique quantique.

Écoutez des membres de la communauté de l'IQ prononcer ce terme dans leur langue maternelle :

Contrairement à ce que son nom laisse penser, la mécanique quantique, ce n’est pas la tendance dernier cri en réparation automobile. En fait, il faut comprendre le terme « mécanique » dans le sens de cadre théorique étudiant les mouvements et l’évolution de systèmes, tout comme on peut parler de « mécanique Newtonienne » pour référer à la physique classique.

Ainsi, la mécanique quantique est la branche de la physique qui s’intéresse aux comportements de la matière et de la lumière qui ne peuvent être expliqués entièrement par la physique classique. Souvent, les effets quantiques se produisent à l'échelle atomique et subatomique, mais on peut parfois observer à notre échelle certains phénomènes qui en découlent.

Développée au début du XXème siècle, elle a permis de comprendre la structure des atomes et particules subatomiques et a introduit des concepts clés tels que la superposition, l’intrication ou encore le principe d’incertitude de Heisenberg. On doit à ces avancées théoriques plusieurs applications de notre quotidien comme les lasers, certains appareils d’imagerie médicale ou encore les transistors, présents dans les ordinateurs et les téléphones intelligents. D’autres applications sont toujours en cours de développement, comme les ordinateurs quantiques qui, à terme, pourraient offrir une puissance de calcul exponentielle pour certains types de problèmes.

Au quotidien, « mesurer » une quantité consiste à comparer la propriété d’un système (par exemple la taille d’une personne) à une grandeur de la même espèce, prise comme étalon. Dans ce cas, la quantité mesurée existe « à priori » et est indépendante de l’appareil de mesure. Évidemment, ce serait une aberration de penser que la mesure modifie l’état du système observé… Et pourtant, ainsi va la mesure pour un système quantique!

De façon générale, on décrit une propriété d’un système quantique par un état formé d’une superposition de toutes les valeurs que cette propriété peut prendre. Par exemple, le spin d’un électron est décrit par une superposition des spins up et down. Quelle est la proportion de spin up et de spin down dans cet état de l’électron? Impossible de le dire!

L’unique façon d’acquérir de l’information sur une propriété d’un système quantique est d’effectuer une mesure. Cependant, cette mesure ne peut retourner qu’une seule des valeurs possibles, par exemple up ou down pour le spin de l’électron. Le résultat d’une mesure est donc probabiliste. Pire encore, la mesure modifie l’état du système observé pour le laisser dans l’état qui a été mesuré. Autrement dit, la mesure détruit toute l’information qui était présente dans l’état de superposition qui prévalait initialement.

La mesure d’une propriété d’un système quantique constitue donc une opération dite « irréversible » : une fois la mesure effectuée, il est impossible d’appliquer une opération inverse qui retournerait le système dans son état préalable. La mesure sur un ordinateur quantique est une opération bien singulière puisque toute les autres opérations – effectuées au moyen de « portes quantiques » – sont réversibles. Un algorithme quantique consiste donc en l’application d’une série d’opérations réversibles qui génèrent un état quantique déterminé, suivi par une mesure qui extrait une seule composante de cet état de façon probabiliste et irréversible !

Écoutez des membres de la communauté de l'IQ prononcer ce terme dans leur langue maternelle :

Si quelqu’un vous demande l’heure, vous aurez le réflexe de la déterminer à l’aide d’une montre. En physique classique, c’est-à-dire en physique à l’échelle humaine, nous sommes familiers avec des grandeurs que nous pouvons mesurer (observer) à l’aide d’appareils, comme la vitesse, la position ou l’énergie.

Cette définition intuitive se complique un peu lorsqu’on passe en physique quantique. Là aussi, les observables correspondent à des grandeurs physiques que l’on peut mesurer, comme la position, la vitesse, l’énergie ou le spin d’une particule. Cependant, on les utilise avec un formalisme différent, c’est-à-dire avec un autre ensemble de définitions et de règles mathématiques décrivant les phénomènes. Dans ce formalisme, les observables sont représentés par des objets mathématiques différents des ceux utilisés en physique classique.

Par conséquent, il existe des observables dits « complémentaires », c’est-à-dire que la mesure de l’un va impacter la mesure de l’autre. Cela mène à des phénomènes pouvant sembler contre-intuitifs. Par exemple, en mécanique quantique, la vitesse et la position sont des observables complémentaires. Ainsi, mesurer la vitesse puis la position d’une particule ne donnera pas le même résultat que le fait de mesurer la position puis la vitesse de cette même particule. Cette propriété est à la base du principe d’incertitude d’Heisenberg, qui dit que l’on ne peut pas connaitre simultanément, avec une précision infinie, la position et la vitesse d’une particule.

Écoutez des membres de la communauté de l'IQ prononcer ce terme dans leur langue maternelle :

Quand on parle de la nature corpusculaire de la lumière, on parle de photons. Qu’est-ce qu’un photon? En quoi consiste-t-il ? Quand et comment a-t-il été découvert?

La nature de la lumière a été le sujet d’un débat mouvementé durant plusieurs siècles pour mener à la compréhension que nous en avons aujourd’hui. En effet, la lumière est plutôt étrange; elle se comporte comme une onde ET comme un ensemble de particules! Bien que la lumière ait des comportements de ces deux phénomènes distincts, c’est son aspect particulaire qui est abordé ici.

C’est en 1905 qu’émerge le concept de photons alors qu’Albert Einstein introduit le principe de « quanta » pour expliquer l’effet photoélectrique, soit le principe d’arracher des électrons à un métal en utilisant l’énergie de la lumière. Einstein nomma «quantum» l’énergie nécessaire à une particule de lumière pour réussir à arracher un électron à un métal particulier. C’est ce quantum qui sera plus tard appelé « photon ». Ainsi, différents types de lumière possédant des énergies particulaires différentes peuvent être utilisés pour arracher des électrons.

Les photons ne composent pas uniquement la lumière visible. En fait, les ondes du spectre électromagnétique sont toutes formées de photons! Les ondes radio, les rayons infrarouges et les rayons gamma en sont des exemples. On ne les voit pas en raison de leur fréquence spécifique, une signature qui les rend invisibles à l’œil humain. Dans la partie visible du spectre, on peut observer ces différences de fréquence partout autour de nous : ce sont ces différences qui font les couleurs!

Bref, les photons sont vraiment partout autour de nous et la nature particulière de la lumière a permis aux scientifiques de l’époque d’ouvrir la boîte de pandore de la mécanique quantique pour donner naissance à une toute nouvelle branche de la physique!

Écoutez des membres de la communauté de l'IQ prononcer ce terme dans leur langue maternelle :

Dans le monde de l’informatique quantique, on entend souvent parler de portes logiques. Mais à quoi ça ressemble, physiquement, des portes logiques et à quoi servent-elles?

Rappelons que dans un ordinateur classique, les unités d’information, qui se nomment « bit » peuvent être soit dans l’état 0, soit dans l’état 1. Dans un ordinateur quantique, les unités d’information, qui se nomment « qubit », peuvent être dans l’état 0 ou 1 – comme l’ordinateur classique – ou encore dans un état superposé 0 et 1.

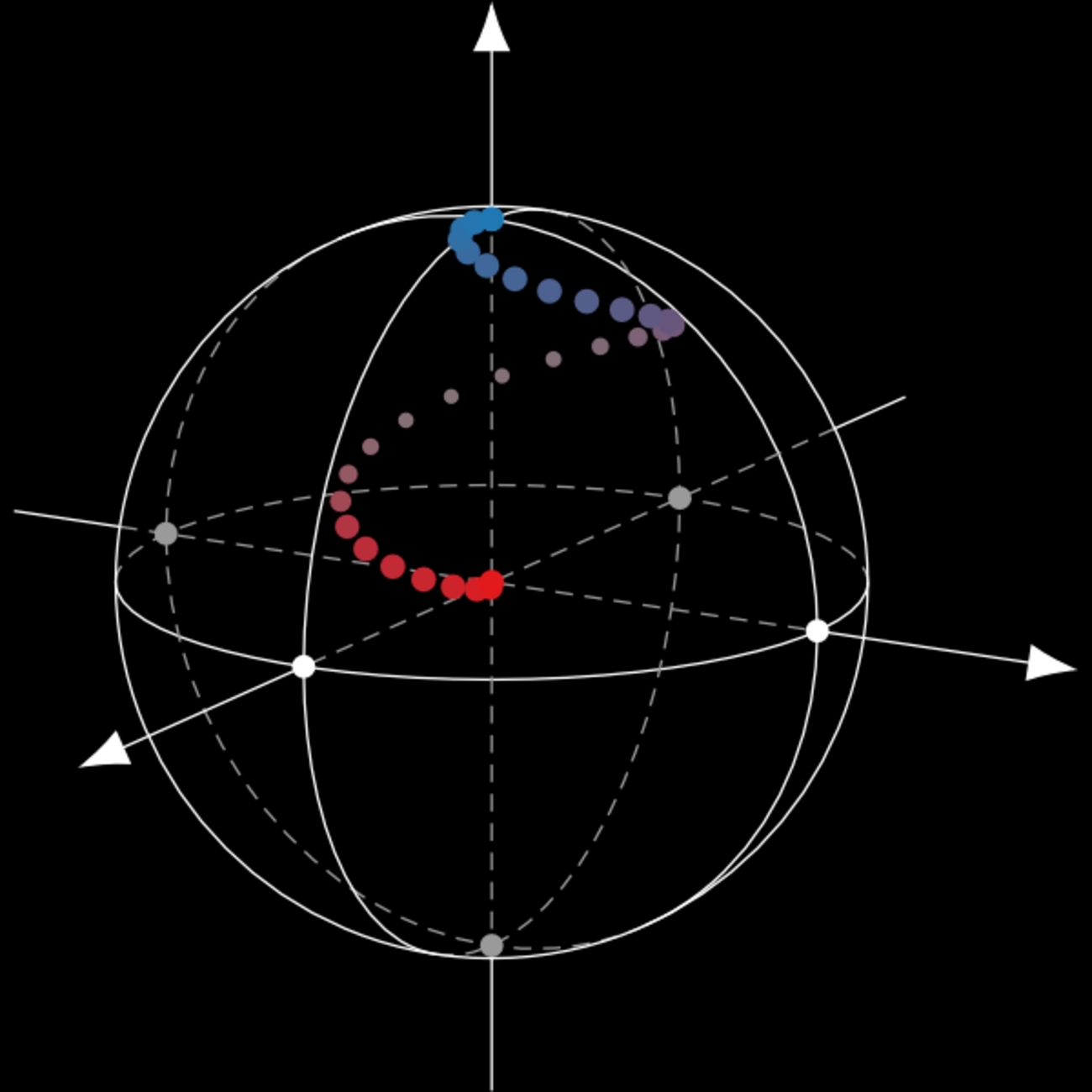
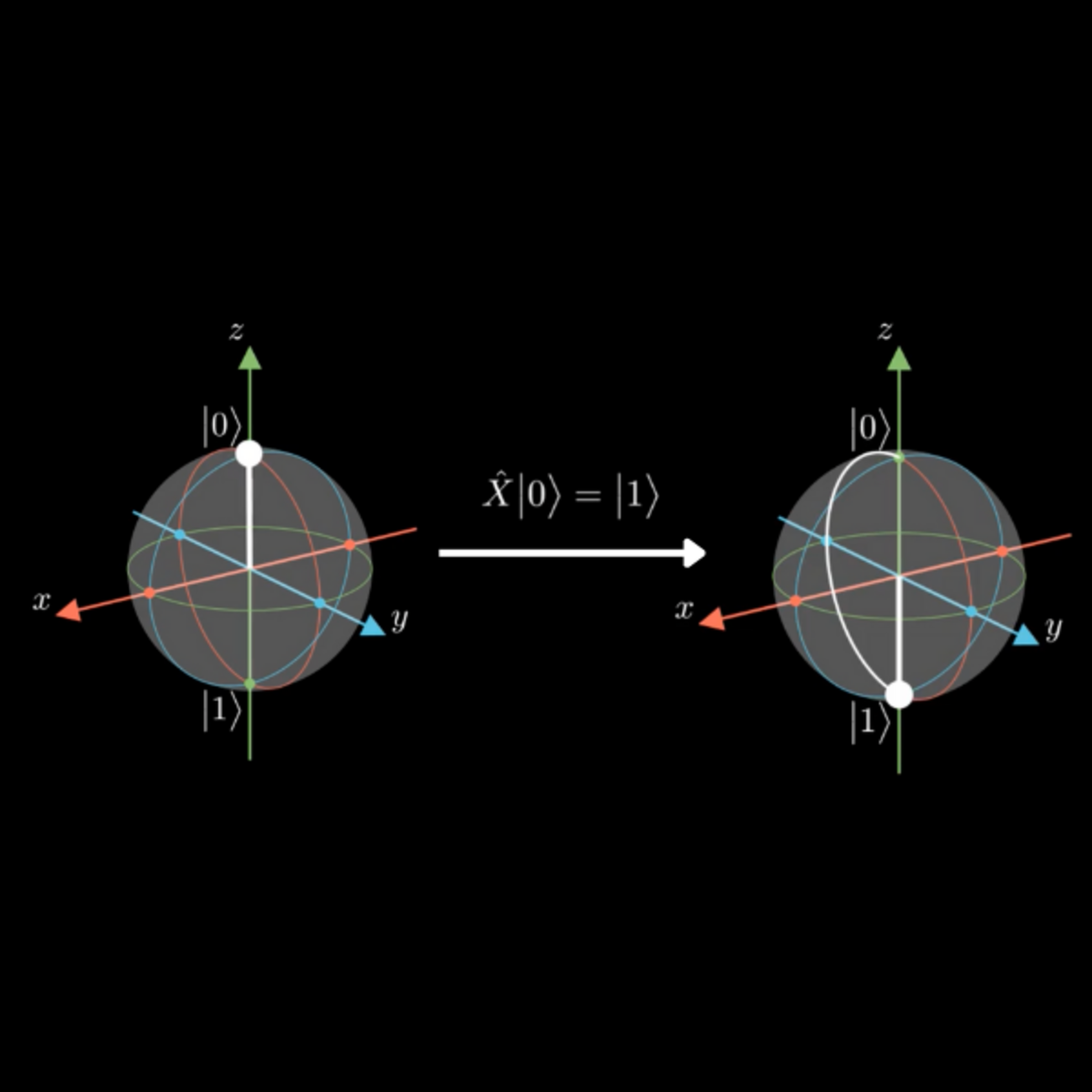
On peut représenter un qubit par un point sur la surface d’une sphère de Bloch à trois dimensions, comme illustré ci-dessous. Les différentes portes logiques modifient l’état quantique d’un qubit en lui imposant une rotation d’un certain angle par rapport à un des axes. Dans l’illustration par exemple, on voit une porte X, aussi appelée porte NOT, qui réalise une rotation de 180 degrés autour de l’axe des x.

Physiquement, l’application des portes logiques dépend de la nature des qubits. Dans le cas des qubits supraconducteurs, comme ceux utilisés par IBM et Google, les portes logiques prennent la forme d’un pulse électromagnétique envoyé sur le qubit, ce qui permet de le faire changer d’état. Chaque porte logique produit la transition souhaitée au moyen d’un pulse ayant une fréquence et une amplitude définies. Ainsi, la fréquence et l’amplitude du pulse de la porte NOT diffèrent par exemple de celles de la porte Z, qui produit quant à elle une rotation de 180 degrés autour de l’axe des z.

Les portes logiques sont donc des opérations utilisées pour programmer des qubits d’information quantique en modifiant leur état. En pratique, il existe plusieurs types de portes logiques quantiques qui font différentes modifications sur l’état des qubits, comme les portes CNOT, Hadamard, SWAP, Toffoli et bien d’autres!

Écoutez des membres de la communauté de l'IQ prononcer ce terme dans leur langue maternelle :

En jouant à « Pile ou Face » avec une pièce de monnaie, on a autant de chances d’obtenir l’un ou l’autre des deux résultats possibles. Si on espère avoir le résultat « pile », on peut dire qu’on a la moitié – ou 50% – des chances de l’obtenir. Cette représentation quantitative de la possibilité d’obtenir un certain résultat, c’est ce qu’on appelle « probabilité ».

Dans l’exemple de la pièce, chaque résultat possible a autant de chance d’être obtenu, mais ce n’est pas toujours le cas! Par exemple, vous pourriez avoir un dé truqué avec 4 côtés portant le chiffre « 1 » et que les autres côtés sont « 2 » et « 3 ». La probabilité d’avoir « 1 » serait alors de 4/6, la probabilité d’avoir « 2 » serait de 1/6 et la probabilité d’avoir « 3 » serait également de 1/6; et pour les chiffres de 4 à 6, la probabilité serait de 0/6.

À noter qu’en additionnant toutes les probabilités ensemble, on obtient 1 (4/6 + 1/6 + 1/6 + 0/6 + 0/6 + 0/6 = 6/6 = 1), c’est-à-dire 100% – ou la totalité – des chances. Autrement dit, si on lance un dé ou une pièce, il est certain qu’on obtiendra… quelque chose!

Le concept de probabilité est fondamental en physique quantique, car un système quantique est décrit par les probabilités de se retrouver dans certains états physiques. Et plus étrange : tant qu’il n’a pas été mesuré, le système quantique peut être en superposition de plusieurs états à la fois.

C’est comme si on invite notre ami, qui est amateur de café et de thé, et qu’on lui offre ces deux options. Sachant qu’il prend 60% du temps du café et 40% du thé, on ne peut pas prédire de quoi il aura le plus envie à un moment précis, vu qu’il peut les vouloir à la fois l’une et l’autre, en superposition. C’est seulement en « prenant la mesure », en le forçant à choisir, qu’on découvre son goût du moment. Avant cela, on ne peut qu’annoncer les probabilités qu’il fasse l’un ou l’autre des choix.

On procède de la même façon pour décrire un système quantique avant une mesure : on doit se contenter de lister les probabilités de ses différents états possibles.

Écoutez des membres de la communauté de l'IQ prononcer ce terme dans leur langue maternelle :

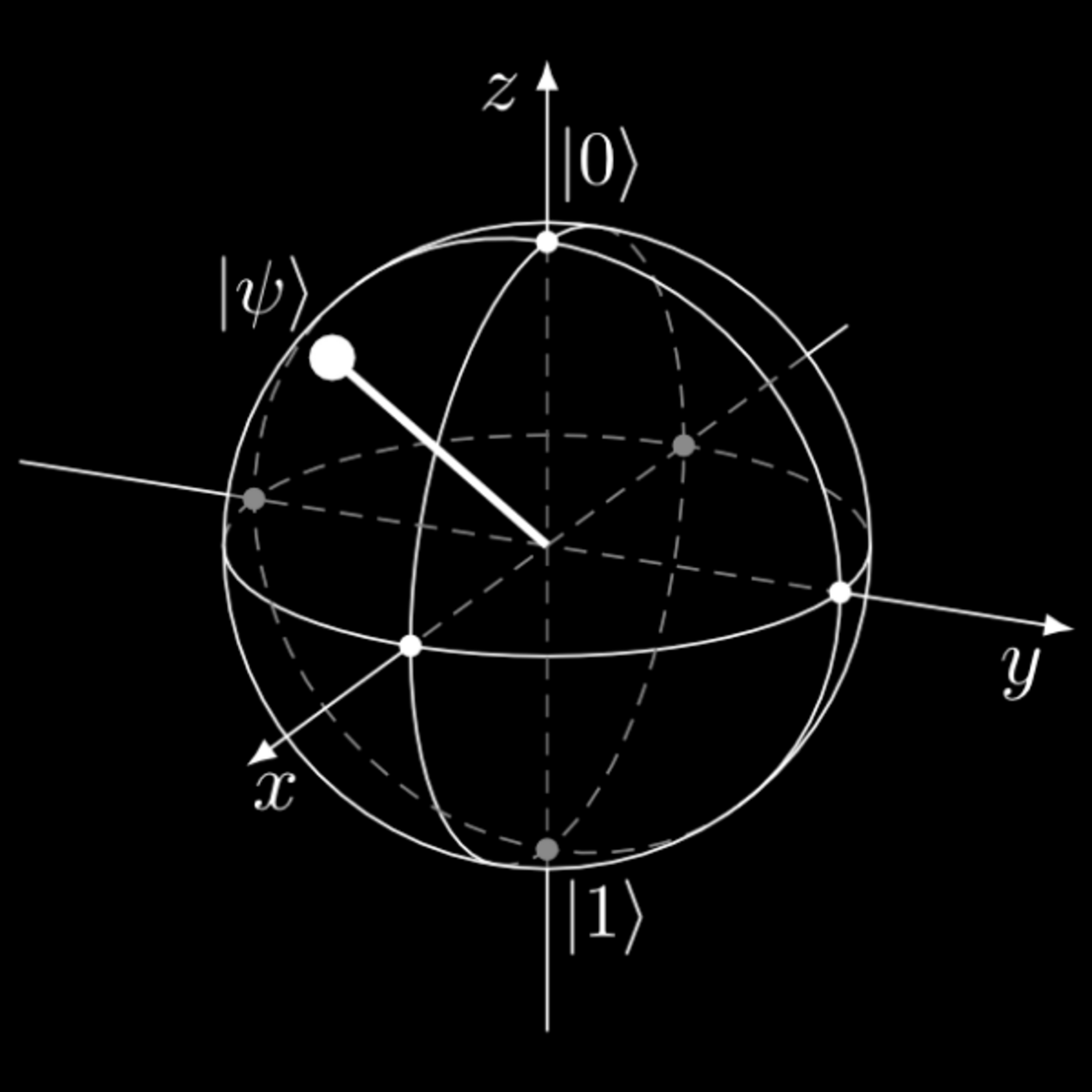
Le qubit est l’unité de base d'un ordinateur quantique qui permet de traiter l'information quantique. Comme dans le bit classique, le qubit peut être placé dans les états 0 et 1. Là où les deux se distinguent, c’est que le qubit peut également être placé dans toutes les superpositions possibles de ces deux états. On représente tous ces états superposés comme un point à la surface d’une sphère de Bloch (voir image).

En connectant plusieurs qubits entre eux, on peut fabriquer un ordinateur quantique. Un groupe de qubits peut exploiter les phénomènes quantiques que sont la superposition, l’intrication et l’interférence pour traiter l’information différemment. Cela ouvre la voie à une nouvelle manière d’effectuer des calculs et de solutionner des problèmes complexes.

À chaque fois qu’on ajoute un qubit à un ordinateur quantique, on double sa puissance de calcul. Ainsi, un ordinateur quantique qui aurait un peu moins de 300 qubits pourrait modéliser parfaitement la molécule de pénicilline. En revanche, cette même tâche nécessiterait un ordinateur classique pouvant traiter 10 bits, une quantité comparable au nombre d’atomes dans l’Univers.

Évidemment la fabrication de qubits dit parfaits pour faire de telles opérations n’est pas simple : le temps de cohérence, la connectivité avec les autres qubits et la fidélité des portes quantiques appliquées sont des défis bien réels pour améliorer la qualité actuelle des qubits et la précision des calculs quantiques.

Il existe présentement plusieurs systèmes physiques potentiels (également appelés architectures) pour réaliser des qubits tels que les qubits supraconducteurs, les qubits de spin ou encore les qubits d’ions piégés. Chaque architecture présente ses avantages et ses défis techniques.

Écoutez des membres de la communauté de l'IQ prononcer ce terme dans leur langue maternelle :

Avez-vous déjà tenté de visualiser ce qui se passe dans vos appareils électroniques? Dans les ordinateurs classiques, les unités d’information, c’est-à-dire les unités que les ordinateurs utilisent pour traiter l’information, sont les bits. Ces derniers peuvent prendre soit la valeur de 0, soit la valeur de 1 pour effectuer les opérations et calculs. De manière similaire, dans les ordinateurs quantiques, les unités d’information se nomment les qubits. Tout comme un bit, un qubit peut prendre la valeur de 0 ou la valeur de 1, mais il peut également être dans une combinaison des deux valeurs en même temps. Ce phénomène quantique se nomme la superposition d’états.

Pour nous aider à visualiser l’idée qu’un qubit peut être 0 et 1 à la fois, on peut recourir à une représentation géométrique appelée la « sphère de Bloch », nommée en l’honneur du physicien Félix Bloch. Imaginez qu’un qubit est au centre de cette sphère et qu’il possède une flèche pointant quelque part à la surface de la sphère. Lorsque la flèche pointe directement vers le haut, on dit que le qubit est dans l’état 0, et lorsqu’elle pointe vers le bas, on a l’état 1. Si la flèche pointe vers un endroit sur la sphère autre que le bas ou le haut, alors le qubit est dans une certaine combinaison des états 0 et 1, de façon superposée.

Pour aller un peu plus loin, si la flèche pointe parfaitement au milieu de la sphère entre le haut (état 0) et le bas (état 1), on dit que le qubit est dans une superposition égale des états 0 et 1. Cependant, si la flèche pointe davantage vers la partie supérieure de la sphère de Bloch, alors le qubit est plus dans l’état 0 que dans l’état 1. La probabilité de le mesurer dans l’état 0 est alors plus grande.

Écoutez des membres de la communauté de l'IQ prononcer ce terme dans leur langue maternelle :

Le moment angulaire est une mesure de la rotation d’un objet autour d’un axe. En physique classique, on distingue deux types de moment angulaire : le moment angulaire orbital, soit la rotation du centre de masse de l’objet, et le moment angulaire intrinsèque qui concerne la rotation autour du centre de masse. Par exemple, la Terre possède un moment angulaire orbital associé à sa rotation d’une période de 1 an autour du Soleil ainsi qu’un moment angulaire intrinsèque associé à sa rotation d’une période de 1 jour autour de son axe.

En mécanique quantique, le moment intrinsèque d’une particule élémentaire est entièrement dicté par le spin de celle-ci. Comme la masse ou la charge, le spin est une propriété interne des particules et sa grandeur est un multiple entier de ½. Par exemple, le boson de Higgs possède un spin 0, l’électron un spin ½, le photon un spin 1. Cette valeur ne peut être modifiée d’aucune façon, mais il est possible d’aligner le spin le long de n’importe quel axe de rotation.

En contrôlant la direction du spin d’une particule quantique, on peut bénéficier de la nature quantique de la matière. Étonnamment, le résultat de la mesure du spin ne peut prendre que des valeurs discrètes. Par exemple, pour une particule de spin ½ telle que l’électron on observera un des deux résultats suivants : +½, ce qu’on appelle spin up, ou -½, soit spin down. Si on aligne le spin le long de l’axe X et qu’on mesure la composante X du spin, on obtiendra +½ avec 100% de probabilité. Cependant, si on mesure la composante Z du spin aligné avec l’axe X, on ne peut pas prédire si on obtiendra +½ ou -½. On sait cependant qu’en moyenne ce sera 0.

Une particule de spin ½ constitue donc un système à deux niveaux qui est utilisé dans certaines architectures de processeurs quantiques pour construire des qubits. Le spin joue également un rôle dans d’autres technologies quantiques telles que les capteurs quantiques.

Écoutez des membres de la communauté de l'IQ prononcer ce terme dans leur langue maternelle :

La superposition est un phénomène quantique qui permet à un système quantique d’être dans deux états en même temps. Ainsi, un électron peut être à deux endroits en même temps et un spin peut être à la fois « up » et « down ». Ce n’est qu’en effectuant une mesure que l’on détermine l’état du système.

Attention : Un système quantique en superposition d’états cesse d’être en superposition au moment de la mesure. Pour certaines quantités, comme le spin, les résultats possibles sont discrets. Ainsi, l’observateur ne pourra jamais obtenir une valeur intermédiaire même si l’état initial était superposé.

Avec l’intrication et l’interférence, la superposition est une des propriétés quantiques qui confère une puissance de calcul exponentielle à l’ordinateur quantique.

Lorsqu'on exécute un circuit quantique, l’état du système de qubits est généralement dans une superposition d’états de tous les résultats possibles, et ce, jusqu’à la mesure. La mesure détermine aléatoirement laquelle de ces possibilités sera le résultat de cette exécution.

En effectuant le même circuit de nombreuses fois, on constatera que certains résultats sont obtenus plus souvent que d’autres. Il faudra alors interpréter les statistiques accumulées pour estimer la réponse du calcul quantique.

Écoutez des membres de la communauté de l'IQ prononcer ce terme dans leur langue maternelle :

Un supraconducteur est un matériau qui permet le passage d’un courant électrique sans aucune résistance, c’est-à-dire sans perte d’énergie ou dissipation de chaleur. La supraconductivité est le phénomène physique qui permet à certains matériaux de manifester cette caractéristique remarquable. Plus qu’un conducteur parfait, un supraconducteur permet également de repousser le champ magnétique. C’est ce qu’on appelle l’effet Meissner.

Pour observer ces propriétés étonnantes, on doit abaisser la température du supraconducteur sous sa température critique, par exemple en le plongeant dans de l’azote liquide (-195°C) ou dans de l’hélium liquide (-269°C) pour des températures encore plus basses. Normalement les électrons se repoussent les uns les autres. Dans un supraconducteur, les basses températures permettent aux électrons de révéler leur nature quantique en les poussant à former des paires de Cooper et abaisser leur niveau d’énergie. C’est pour cette raison qu’on dit que la supraconductivité est une propriété quantique de la matière.

Bien qu’on retrouve déjà la supraconductivité dans le fonctionnement de l’imagerie par résonance magnétique (IRM), les matériaux supraconducteurs ont le potentiel de grandement améliorer le stockage et l’efficacité des réseaux de distribution d’électricité ainsi que les génératrices électriques à l’intérieur des turbines éoliennes. Finalement, la supraconductivité est au cœur de plusieurs architectures de qubits et joue un rôle important en informatique quantique.

Sans conteste, l’aspect le plus spectaculaire de la supraconductivité est la répulsion du champ magnétique qui donne lieu à la lévitation magnétique.

Écoutez des membres de la communauté de l'IQ prononcer ce terme dans leur langue maternelle :

Avez-vous déjà vu un transistor? Pourtant, vous en avez à portée de main si vous lisez ces lignes! En effet, tous les appareils électroniques modernes fonctionnent grâce à une multitude de transistors cachés à l’intérieur. Ceux-ci ne sont pas directement quantiques, mais c'est parce qu'on a compris un phénomène quantique qu'on a pu améliorer cette technologique classique.

Fabriqués avec des matériaux semi-conducteurs, les transistors peuvent être contrôlés afin de laisser passer ou non un courant électrique, un peu comme des tuyaux d’arrosage qu’on ouvre ou ferme au besoin avec une valve.

Avec les progrès dans les méthodes de fabrication, les transistors ont énormément rapetissé, passant progressivement de plusieurs centimètres en 1947 à quelques nanomètres de nos jours. Ils sont désormais plus petits qu’un virus! Cela permet d'en mettre plus par appareil, augmentant ainsi leur puissance.

Le hic, c’est qu’en rapetissant les transistors, on s’est rapidement rendu à l’échelle où se produisent des phénomènes quantiques parfois très surprenants, tels que l’effet tunnel. Ceci permet à de minuscules objets, tels que les électrons d’un courant électrique, de passer à travers des obstacles censés être infranchissables. C’est comme si un peu d’eau passait soudainement à travers la valve du tuyau d’arrosage, même si elle est complètement fermée.

Avant de comprendre ce phénomène, on ne pouvait pas fabriquer de bonnes puces de très petite taille: il y avait trop de « fuites » du courant qui brouillaient les signaux et qui faisait rapidement surchauffer les appareils. C’est seulement en comprenant l’effet tunnel qu’on a pu recommencer à progresser dans la course à la miniaturisation de l’électronique. On est alors passé de 10 transistors par puce électronique en 1970 à des milliards aujourd’hui!

Pour aller plus loin, des scientifiques explorent comment exploiter l’effet tunnel plutôt que de l’éviter, ce qui pourrait repousser davantage la limite de miniaturisation. On pourrait alors obtenir un transistor quantique ou encore une nouvelle façon de fabriquer des qubits!

Écoutez des membres de la communauté de l'IQ prononcer ce terme dans leur langue maternelle :

Termes quantiques

Algorithme

Algorithme de Grover

Algorithme de Shor

Atome

Chat de Schrödinger

Cuprate

Décohérence

Dualité onde-corpuscule

Émergence

Énergie

Équation de Schrödinger

Fentes de Young

Incertitude

Intrication

Matériau quantique

Matrice

Mécanique quantique

Mesure

Observable

Photon

Portes logiques quantiques

Probabilité

Qubit

Sphère de Bloch

Spin

Superposition

Supraconductivité

Transistor