Tracer la route de l’information dans le cerveau avec QAOA
Par Harshana Runjeet, étudiante au baccalauréat en physique
Café, thé noir ou jus d’orange? Notre vie se tisse au gré des décisions que nous prenons à chaque instant. Lorsque la situation est trop complexe, nous dressons une liste des arguments pour et contre afin de faire un choix éclairé. Les problèmes de décisions se retrouvent également en informatique, autant classique que quantique. Des algorithmes constituent l’ensemble des instructions données à un ordinateur afin que ce dernier puisse faire un choix et résoudre le problème donné; l’un d’entre eux se nomme QAOA (pour Quantum Approximate Optimization Algorithm) !
Cartographier le cerveau, projet d’envergure
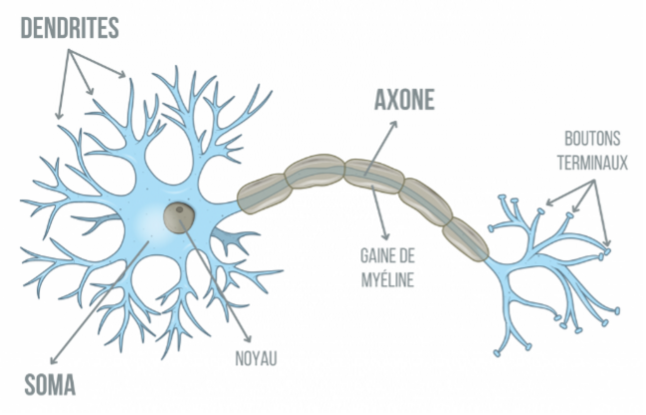
Le cerveau est constitué de 100 milliards de cellules nerveuses, les neurones, et chacun de ses neurones aurait plus de mille connexions, ce qui rend le réseau du cerveau humain très complexe.
Pour essayer de l’étudier, plusieurs méthodes ont été développées, dont l’imagerie par résonance magnétique de diffusion (dMRI). Cette technique tire profit de la grande présence de l’eau dans le cerveau en étudiant sa diffusion. Après tout, l’eau est une substance qui prend la forme de son contenant, comme le disait Bruce Lee! C’est aussi vrai dans les neurones, où elle suivra également la forme des cylindres (les axones) et se diffusera le long de la direction donnée par les neurones environnants. Ainsi, en ayant un aperçu du mouvement de l’eau, il est possible d’avoir une idée des chemins que prend l’information le long des neurones.
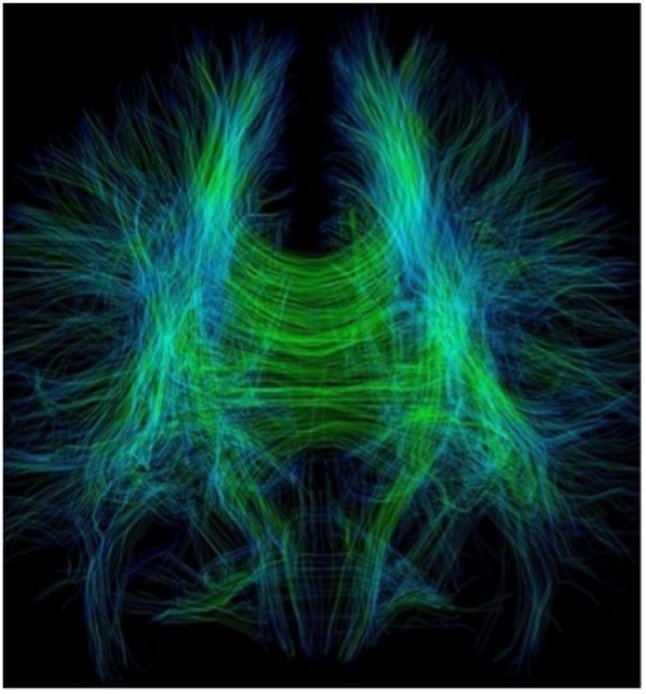
Des appareils sont donc conçus de manière à capter la diffusion de l’eau dans une direction donnée, permettant de tracer une image comportant différentes teintes de gris associées à l’intensité de diffusion pour une tranche en deux dimensions du cerveau. En répétant l’opération avec plusieurs tranches et en assemblant ces images, on obtient une image tridimensionnelle du câblage neuronal, telle qu’à la figure 2.
Trouver le chemin optimal avec des graphes
Supposons que, pour un point de départ et d’arrivée dans la matière grise, l’information emprunte le chemin où la diffusion de l’eau se fait le plus aisément. On obtient alors un problème pouvant être modélisé mathématiquement, soit la maximisation des intensités de diffusion d’un point à un autre, afin de trouver le chemin emprunté par l’information.
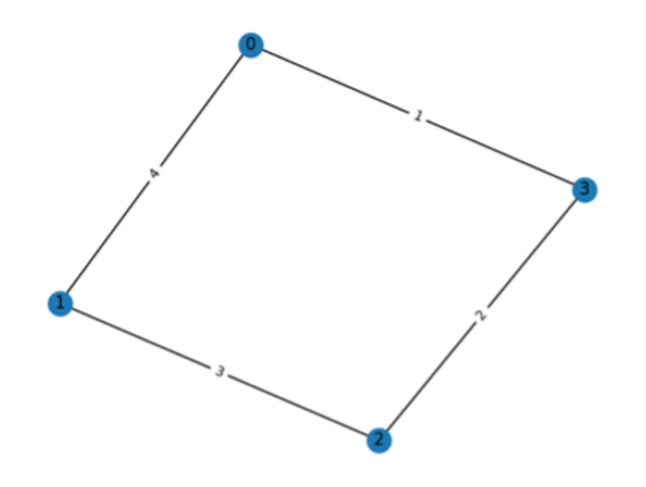
Ce type de problème permet de représenter les images de diffusion comme un graphe pondéré qui est un ensemble de nœuds (les pixels dans les images de tranches de cerveaux) reliés par des arêtes, avec un certain poids associé à l’intensité de diffusion entre nœuds voisins.
Il ne reste qu’à définir un test qui indique le poids total associé à un chemin donné. Ce test sera en fait une fonction de coût qu’un algorithme peut évaluer dans le but de calculer le poids de tous les chemins différents et de déterminer le chemin avec le poids maximal. Il est important d’inclure certaines contraintes dans cette fonction de coût, afin que l’algorithme puisse choisir un chemin réaliste. Sinon, le chemin maximisant la diffusion dans notre cas serait toujours celui qui comprend toutes les arêtes du graphe, et ce scénario n’est nullement réaliste.
C’est ici qu’un ordinateur classique peut avoir du mal : avec 100 milliards de neurones interconnectés les uns les autres, les possibilités de chemins différents sont si énormes qu’il lui est impossible de trouver une solution dans un délai raisonnable!
QAOA à la rescousse!
En revanche, les ordinateurs quantiques peuvent être d’une grande aide dans ce contexte, grâce à l’exploitation de propriétés quantiques incluant la superposition d’états.En effet, les bits quantiques, ou qubits, peuvent encoder les états 0 ou 1 (jusque-là comme les ordinateurs classiques), mais aussi 0 et 1 en superposition. On peut alors effectuer le calcul avec 0 et celui avec 1 en parallèle, et comme plusieurs possibilités sont testées en même temps, on trouve plus rapidement la meilleure solution. C’est ainsi que fonctionne QAOA, un algorithme quantique qui résout notamment des problèmes de minimisation dans des graphes.
Reprenons l’exemple d’un graphe modélisant la diffusion d’eau dans un cerveau. L’algorithme QAOA prend en entrée un nœud de départ et de fin. À partir de cela, chaque arête du graphe est assignée à un qubit initialisé à l’état 0. Ensuite, un circuit quantique est construit à partir de la fonction de coût, où on s’assure de passer une seule fois par le nœud de départ et de fin (en contraignant les nœuds de départ et de fin à une connexion chacun). Il faut en outre passer aucune ou deux fois par un nœud intermédiaire (contrainte de nombre pair de connexions), car un nœud intermédiaire est relié au nœud précédent ainsi qu’au suivant.
Une fois qu’on a programmé notre circuit avec les contraintes souhaitées, on lance le calcul et on mesure le résultat : les qubits mesurés dans l’état 1 indiquent que cette connexion fait partie du chemin; alors que les qubits dans l’état 0 indiquent les connexions non retenues parmi les chemins possibles. Autrement dit, QAOA calcule en simultané les poids des différents chemins possibles et il détermine la solution optimale, c’est-à-dire le chemin qui maximise la diffusion d’eau dans le cerveau.
Tout ceci semble idéal, mais il reste encore un grand défi technique avant de pouvoir cartographier le cerveau avec des graphes de milliers d’arêtes et de nœuds ! À ce jour, les ordinateurs quantiques ont une capacité limitée à une centaine de qubits, qui sont par ailleurs très bruyants. Il est donc impossible pour le moment de solutionner un problème complexe comme la recherche d’un chemin optimal à l’échelle globale du cerveau.
De plus, il y a encore des difficultés à résoudre quant aux paramètres du code de QAOA et de la fonction coût qu’on lui attribue. Pour le moment, les paramètres sont sensibles à chaque graphe donné et notre algorithme ne fonctionne plus aussi bien au-delà de 10 connexions, alors il reste à déterminer comment trouver un chemin optimal pour un cas général avec un chemin plus long. Bref, il faudra encore attendre un peu pour que la quantique perce les mystères du câblage de notre cerveau!