News
Two scientists of the IQ make progress on manipulating the fascinating property of quantum entanglement
Pr Stefanos Kourtis and Jeremy côté
Photo : Michel Caron UdeSThe 2022 Nobel Prize in Physics laureate for quantum entanglement, Alain Aspect and his team demonstrated that this quantum property exists! This is not where the story ends: There are other mysteries surrounding quantum entanglement awaiting to be explored with a large potential of applications, including in quantum cryptography and communication. On this research path, Jeremy Côté and his PhD supervisor Prof. Stefanos Kourtis shared their recent experience, driven by both passion and patience, which led to the publication of the theoretical research paper “Entanglement phase transition with spin glass criticality” in Physical Review Letters. Six months later, the research duo also published an experimental paper entitled “Qubit vitrification and entanglement criticality on a quantum simulator” in the advanced multidisciplinary research journal Nature Communications.
Doctoral student in physics and member of IQ’s science outreach committee, Jeremy Côté was awarded by the Regroupement des étudiants-chercheurs en sciences de l’Université de Sherbrooke for his commitment through his Twitter account (@HandwavingComic), which humorously explains the reality of scientists. Jeremy enthusiastically describes: ” Much like you can enjoy the emotional pull of a piece of music without knowing the intricacies in creating the piece, you can enjoy science without being an expert”
IQ’s Quantum AlgoLab director, Prof. Stefanos Kourtis proudly explains the distinctive feature of their project: “With the access to quantum systems provided by the AlgoLab, once the theory was formulated, Jeremy was able to conduct the required experiments himself that prove our theory. Thus, the experimental verification of our theory happened very quickly. Having such direct access to the quantum world allows us to do research that was impossible to imagine until recently.”
Quantum technologies are at the very heart of the second quantum revolution that will lead to new applications. Understanding the interactions between the bits of a quantum computer, called qubits, especially when taking measurements, is essential to harness the potential of quantum computing. Generally, scientists try to isolate a quantum system and minimize its interaction with its environment before the final measurement. But the isolation is not perfect, and one can model this interaction with a quantum simulator. In this context, the preliminary measurements serve as a mechanism of interaction between the quantum system and its environment. Performing these measurements weakens the entangled links between the qubits of the simulator. In other words, it makes their quantum states less correlated, and can even cause a major loss of information, up to complete decoherence. The studies already undertaken around this problem in quantum computing use measurements and quantum programming tools, called logic gates, which are entirely random. Until recently, the entanglement rate evolution of a given class of quantum states during the measurement was not sufficiently studied, and more importantly, not properly quantified.
What makes Jeremy and Stefanos’ work original is the precision of the structure. In their first project, they use a theory of statistical mechanics – the theory of spin glasses, recognized by the Nobel Prize in Physics 2021 – to establish an exact description of a phase transition in the entanglement of qubits. Their second project was a structured experiment design based on the previously chosen theory. The challenge of this experiment was to find the perfect balance between the theory and the constraints of current quantum simulators. The measurements are then optimized to have the highest number of results with the lowest error rate.
The algorithm for their study consists of a circuit of logic gates applied to qubits and in return, at the output, we obtain an intricate system of qubits in superposition. This circuit can be represented by a mathematical object called a matrix. This consists of an array of 0 and 1 entries, where each column represents a spin, an internal property of the particles, and each row represents an interaction between 3 spins. In the figure below, the logic gates with a “1” correspond to a 1 in the matrix, and the other gate corresponds to a 0.
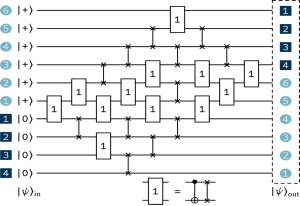
Jeremy and Stefanos also use this matrix to ensure the accuracy of their experiments as well as to detect and eliminate errors made by the quantum computer during these calculations. During the experiment, Jeremy progressively measures up to 48 qubits. After a precise number of qubits measured, the qubits start to adopt a different pattern of behavior and a transition in qubit entanglement emerges. They discover a new phase transition, locate the transition point and evaluate its critical exponent to better identify and understand this transition. The experiment proves the entanglement rate decreases discontinuously during the measurements.
The work of Jeremy and Stefanos represents a big step towards a better understanding and control over quantum entanglement, a fascinating property. And these are probably not the last quantum secrets that these two researchers will unveil to us.
