Developing error correction codes

Fault-tolerant quantum computation, quantum error-correction – these terms are used to illustrate one of the challenges holding back the advent of quantum computing.

Many scientists are working actively to identify error-correction algorithms. Maxime Tremblay, a PhD student at the Institut quantique, is one of them.

The publication Constant-overhead quantum error correction with thin planar connectivity in Physical Review Letters is the result of research conducted during an internship at Microsoft with researchers Nicolas Delfosse and Michael E. Beverland, co-authors of the article.

” Those people who design and implement qubits are very good at what they do, except that a perfect qubit does not exist. So, let’s say an operation, is off target by a tiny margin because of noise, imagine that operation being repeated thousands of times, a small error that accumulates can cause it to miss the target significantly.”

When participating in a competition entitled My Thesis in 180 Seconds, he used the image of a railroad network. “If, for instance, this network connected all the major cities in Quebec to Montreal, what would happen if a snowstorm hit? What would happen if a snowstorm interrupted the service between Sherbrooke and Montreal? Sherbrooke would be cut off from the rest of Quebec. Small disruptions to the network should not be allowed to have a significant impact on the whole.

Plans to connect the components of the quantum computer. 

As additional components are added to the quantum computer, the idea is to avoid the multiplication of errors to maximize reliability while also minimizing resources. Taking the railroad analogy, it is possible to build railroads that would connect all the cities together, which would end up generating exorbitant costs given the multiplicity of networks.

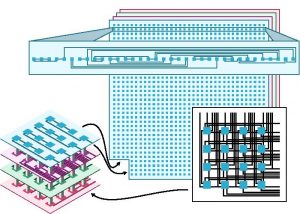
Maxime Tremblay explains the publication in these terms. “To achieve this balance, we used methods that provide excellent connection patterns. They allow us to link qubits with fewer connections between them, while restricting the amount of errors.”

Developing mathematical models to link qubits together is the first step, but the job is not yet completed. Tremblay describes the next step: ” We must then measure the system and measuring a quantum system is a complicated task, there are many rules to observe. The next question we asked ourselves was: now that we know that these connectivity patterns are very robust and low cost, can we measure them efficiently?”

Measuring the state of the system ensures reliable operations or, if necessary, makes some adjustments to regain that reliability. This measurement must also be done very quickly to maintain efficiency and thus take advantage of the full potential of quantum computing.

“We found an algorithm that is optimal in terms of time and resources to probe the state of the system. We developed the algorithm and demonstrated with mathematical results that it was optimal, that it is not possible to do better.”

Nicholas Delfosse “A major obstacle to the design of a large scale quantum computer is the massive cost of quantum error correction. Most of what a quantum computer does is correcting errors to guarantee that the result of the computation is correct. Maxime did a fantastic work during his internship in our team at Microsoft. This opens the way to a new kind of quantum computer architecture which can significantly reduce the cost of quantum error correction.”

And this algorithm can be applied to any qubit architecture.

For co-author Nicholas Delfosse, Principal Researcher at Microsoft Quantum and former postdoc in David Poulin’s group, Maxime’s work is simply remarkable. “A major obstacle to the design of a large scale quantum computer is the massive cost of quantum error correction. Most of what a quantum computer does is correcting errors to guarantee that the result of the computation is correct. Maxime did a fantastic work during his internship in our team at Microsoft. This opens the way to a new kind of quantum computer architecture which can significantly reduce the cost of quantum error correction.”

What differentiates the research of Maxime Tremblay and his colleagues is the method chosen, as he describes it : “We used methods that come from graph theory for connectivity and patterns to design the circuits and chips. We were largely inspired by methods used in classical computing, which works with millions of processors placed on tiny chips. It is impossible to overlap two processors. To use the train analogy once again, you can’t put rails through the buildings or place them on top of each other. We used mathematical theories from classical computing to apply them to quantum computing.”